
°æƒø°ø…Ë{an}∫Õ{bn} «¡Ω∏ˆµ»≤Ó ˝¡–£¨º«cn=max{b1©Åa1n£¨b2©Åa2n£¨°≠£¨bn©Åann}£®n=1£¨2£¨3£¨°≠£©£¨∆‰÷–max{x1 £¨ x2 £¨ °≠£¨xs}±Ì æx1 £¨ x2 £¨ °≠£¨xs’‚s∏ˆ ˝÷–◊Ó¥Ûµƒ ˝£Æ£®13∑÷£©
£®1£©»Ùan=n£¨bn=2n©Å1£¨«Ûc1 £¨ c2 £¨ c3µƒ÷µ£¨≤¢÷§√˜{cn} «µ»≤Ó ˝¡–£ª
£®2£©÷§√˜£∫ªÚ’þ∂‘»Œ“‚’˝ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨µ±n°ðm ±£¨ ![]() £æM£ªªÚ’þ¥Ê‘⁄’˝’˚ ˝m£¨ πµ√cm £¨ cm+1 £¨ cm+2 £¨ °≠ «µ»≤Ó ˝¡–£Æ
£æM£ªªÚ’þ¥Ê‘⁄’˝’˚ ˝m£¨ πµ√cm £¨ cm+1 £¨ cm+2 £¨ °≠ «µ»≤Ó ˝¡–£Æ
°æ¥∞∏°ø
£®1£©
Ω‚£∫ a1=1£¨a2=2£¨a3=3£¨b1=1£¨b2=3£¨b3=5£¨
µ±n=1 ±£¨c1=max{b1©Åa1}=max{0}=0£¨
µ±n=2 ±£¨c2=max{b1©Å2a1£¨b2©Å2a2}=max{©Å1£¨©Å1}=©Å1£¨
µ±n=3 ±£¨c3=max{b1©Å3a1£¨b2©Å3a2£¨b3©Å3a3}=max{©Å2£¨©Å3£¨©Å4}=©Å2£¨
œ¬√Ê÷§√˜£∫∂‘n° N*£¨«“n°ð2£¨∂º”–cn=b1©Åna1£¨
µ±n° N*£¨«“2°Ðk°Ðn ±£¨
‘Ú£®bk©Ånak£©©Å£®b1©Åna1£©£¨
=[£®2k©Å1£©©Ånk]©Å1+n£¨
=£®2k©Å2£©©Ån£®k©Å1£©£¨
=£®k©Å1£©£®2©Ån£©£¨”…k©Å1£æ0£¨«“2©Ån°Ð0£¨
‘Ú£®bk©Ånak£©©Å£®b1©Åna1£©°Ð0£¨‘Úb1©Åna1°ðbk©Ånak£¨
“Ú¥À£¨∂‘n° N*£¨«“n°ð2£¨cn=b1©Åna1=1©Ån£¨
cn+1©Åcn=©Å1£¨
°ýc2©Åc1=©Å1£¨
°ýcn+1©Åcn=©Å1∂‘n° N*æ˘≥…¡¢£¨
°ý ˝¡–{cn} «µ»≤Ó ˝¡–£ª
£®2£©
÷§√˜£∫…Ë ˝¡–{an}∫Õ{bn}µƒπ´≤Ó∑÷±Œ™d1£¨d2£¨œ¬√Êøº¬«µƒcn»°÷µ£¨
”…b1©Åa1n£¨b2©Åa2n£¨°≠£¨bn©Åann£¨
øº¬«∆‰÷–»Œ“‚bi©Åain£¨£®i° N*£¨«“1°Ði°Ðn£©£¨
‘Úbi©Åain=[b1+£®i©Å1£©d1]©Å[a1+£®i©Å1£©d2]°¡n£¨
=£®b1©Åa1n£©+£®i©Å1£©£®d2©Åd1°¡n£©£¨
œ¬√Ê∑÷d1=0£¨d1£æ0£¨d1£º0»˝÷÷«ÈøˆΩ¯––Ã÷¬€£¨
¢Ÿ»Ùd1=0£¨‘Úbi©Åain®T£®b1©Åa1n£©+£®i©Å1£©d2£¨
µ±»Ùd2°Ð0£¨‘Ú£®bi©Åain£©©Å£®b1©Åa1n£©=£®i©Å1£©d2°Ð0£¨
‘Ú∂‘”⁄∏¯∂®µƒ’˝’˚ ˝n∂¯—‘£¨cn=b1©Åa1n£¨¥À ±cn+1©Åcn=©Åa1£¨
°ý ˝¡–{cn} «µ»≤Ó ˝¡–£ª
µ±d1£æ0£¨£®bi©Åain£©©Å£®bn©Åann£©=£®i©Å1£©d2°Ð0£¨
‘Ú∂‘”⁄∏¯∂®µƒ’˝’˚ ˝n∂¯—‘£¨cn=bn©Åann=bn©Åa1n£¨
¥À ±cn+1©Åcn=d2©Åa1£¨
°ý ˝¡–{cn} «µ»≤Ó ˝¡–£ª
¥À ±»°m=1£¨‘Úc1£¨c2£¨°≠£¨ «µ»≤Ó ˝¡–£¨√¸Ã‚≥…¡¢£ª
¢⁄»Ùd1£æ0£¨‘Ú¥À ±©Åd1n+d2Œ™“ª∏ˆπÿ”⁄nµƒ“ª¥ŒœÓœµ ˝Œ™∏∫ ˝µƒ“ª¥Œ∫Ø ˝£¨
π ±ÿ¥Ê‘⁄m° N*£¨ πµ√n°ðm ±£¨©Åd1n+d2£º0£¨
‘Úµ±n°ðm ±£¨£®bi©Åain£©©Å£®b1©Åa1n£©=£®i©Å1£©£®©Åd1n+d2£©°Ð0£¨£®i° N*£¨1°Ði°Ðn£©£¨
“Ú¥Àµ±n°ðm ±£¨cn=b1©Åa1n£¨
¥À ±cn+1©Åcn=©Åa1£¨π ˝¡–{cn}¥”µ⁄mœÓø™ ºŒ™µ»≤Ó ˝¡–£¨√¸Ã‚≥…¡¢£ª
¢€»Ùd1£º0£¨¥À ±©Åd1n+d2Œ™“ª∏ˆπÿ”⁄nµƒ“ª¥ŒœÓœµ ˝Œ™’˝ ˝µƒ“ª¥Œ∫Ø ˝£¨
π ±ÿ¥Ê‘⁄s° N*£¨ πµ√n°ðs ±£¨©Åd1n+d2£æ0£¨
‘Úµ±n°ðs ±£¨£®bi©Åain£©©Å£®bn©Åann£©=£®i©Å1£©£®©Åd1n+d2£©°Ð0£¨£®i° N*£¨1°Ði°Ðn£©£¨
“Ú¥À£¨µ±n°ðs ±£¨cn=bn©Åann£¨
¥À ±= ![]() =©Åan+
=©Åan+ ![]() £¨
£¨
=©Åd2n+£®d1©Åa1+d2£©+ ![]() £¨
£¨
¡Ó©Åd1=A£æ0£¨d1©Åa1+d2=B£¨b1©Åd2=C£¨
œ¬√Ê÷§√˜£∫ ![]() =An+B+
=An+B+ ![]() ∂‘»Œ“‚’˝’˚ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√n°ðm£¨
∂‘»Œ“‚’˝’˚ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√n°ðm£¨ ![]() £æM£¨
£æM£¨
»ÙC°ð0£¨»°m=[ ![]() +1]£¨[x]±Ì æ≤ª¥Û”⁄xµƒ◊Ó¥Û’˚ ˝£¨
+1]£¨[x]±Ì æ≤ª¥Û”⁄xµƒ◊Ó¥Û’˚ ˝£¨
µ±n°ðm ±£¨ ![]() °ðAn+B°ðAm+B=A[
°ðAn+B°ðAm+B=A[ ![]() +1]+B£æA
+1]+B£æA ![]() +B=M£¨
+B=M£¨
¥À ±√¸Ã‚≥…¡¢£ª
»ÙC£º0£¨»°m=[ ![]() ]+1£¨
]+1£¨
µ±n°ðm ±£¨
![]() °ðAn+B+
°ðAn+B+ ![]() °ðAm+B+C£æA
°ðAm+B+C£æA ![]() +B+C
+B+C ![]() °ðM©ÅC©ÅB+B+C=M£¨
°ðM©ÅC©ÅB+B+C=M£¨
¥À ±√¸Ã‚≥…¡¢£¨
“Ú¥À∂‘»Œ“‚’˝ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√µ±n°ðm ±£¨ ![]() £æM£ª
£æM£ª
◊€∫œ“‘…œ»˝÷÷«Èøˆ£¨√¸Ã‚µ√÷§£Æ
°æΩ‚Œˆ°ø£®1.£©∑÷±«Ûµ√a1=1£¨a2=2£¨a3=3£¨b1=1£¨b2=3£¨b3=5£¨¥˙»Îº¥ø…«Ûµ√c1 £¨ c2 £¨ c3£ª”…£®bk©Ånak£©©Å£®b1©Åna1£©°Ð0£¨‘Úb1©Åna1°ðbk©Ånak £¨ ‘Úcn=b1©Åna1=1©Ån£¨cn+1©Åcn=©Å1∂‘n° N*æ˘≥…¡¢£ª
£®2.£©”…bi©Åain=[b1+£®i©Å1£©d1]©Å[a1+£®i©Å1£©d2]°¡n=£®b1©Åa1n£©+£®i©Å1£©£®d2©Åd1°¡n£©£¨∑÷¿ýÃ÷¬€d1=0£¨d1£æ0£¨d1£º0»˝÷÷«ÈøˆΩ¯––Ã÷¬€∏˘æðµ»≤Ó ˝¡–µƒ–‘÷ £¨º¥ø…«Ûµ√ πµ√cm £¨ cm+1 £¨ cm+2 £¨ °≠ «µ»≤Ó ˝¡–£ª…Ë ![]() =An+B+
=An+B+ ![]() ∂‘»Œ“‚’˝’˚ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√n°ðm£¨
∂‘»Œ“‚’˝’˚ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√n°ðm£¨ ![]() £æM£¨∑÷¿ýÃ÷¬€£¨≤…”√∑≈Àı∑®º¥ø…«Ûµ√“Ú¥À∂‘»Œ“‚’˝ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√µ±n°ðm ±£¨
£æM£¨∑÷¿ýÃ÷¬€£¨≤…”√∑≈Àı∑®º¥ø…«Ûµ√“Ú¥À∂‘»Œ“‚’˝ ˝M£¨¥Ê‘⁄’˝’˚ ˝m£¨ πµ√µ±n°ðm ±£¨ ![]() £æM£Æ
£æM£Æ
°æøºµ„æ´Œˆ°ø∏˘æðƒøµƒ“—÷™Ãıº˛£¨¿˚”√µ»≤Óπÿœµµƒ»∑∂®µƒœýπÿ÷™ ∂ø…“‘µ√µΩŒ µƒ¥∞∏£¨–Ë“™’∆Œ’»Áπ˚“ª∏ˆ ˝¡–¥”µ⁄2œÓ∆£¨√ø“ªœÓ”ÎÀ¸µƒ«∞“ªœÓµƒ≤Óµ»”⁄Õ¨“ª∏ˆ≥£ ˝£¨º¥![]() £≠
£≠![]() =d £¨£®n°ð2£¨n° N
=d £¨£®n°ð2£¨n° N![]() £©ƒ«√¥’‚∏ˆ ˝¡–æÕΩ–◊ˆµ»≤Ó ˝¡–£Æ
£©ƒ«√¥’‚∏ˆ ˝¡–æÕΩ–◊ˆµ»≤Ó ˝¡–£Æ


 ÓºŸœŒΩ”ΩÃ≤ƒ∆⁄ƒ© ÓºŸ‘§œ∞Œ‰∫∫≥ˆ∞Ê…Áœµ¡–¥∞∏
ÓºŸœŒΩ”ΩÃ≤ƒ∆⁄ƒ© ÓºŸ‘§œ∞Œ‰∫∫≥ˆ∞Ê…Áœµ¡–¥∞∏ ºŸ∆⁄◊˜“µ ÓºŸ≥…≥§¿÷‘∞–¬ΩÆ«ý…ŸƒÍ≥ˆ∞Ê…Áœµ¡–¥∞∏
ºŸ∆⁄◊˜“µ ÓºŸ≥…≥§¿÷‘∞–¬ΩÆ«ý…ŸƒÍ≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥¬√”Œ∞Æ∫√’þº∆ªÆ¥”3∏ˆ—«÷Þπ˙º“A1 £¨ A2 £¨ A3∫Õ3∏ˆ≈∑÷Þπ˙º“B1 £¨ B2 £¨ B3÷–—°‘Ò2∏ˆπ˙º“»•¬√”Œ£Æ
£®¢Ò£©»Ù¥”’‚6∏ˆπ˙º“÷–»Œ—°2∏ˆ£¨«Û’‚2∏ˆπ˙º“∂º «—«÷Þπ˙º“µƒ∏≈¬ £ª
£®¢Ú£©»Ù¥”—«÷Þπ˙º“∫Õ≈∑÷Þπ˙º“÷–∏˜»Œ—°1∏ˆ£¨«Û’‚2∏ˆπ˙º“∞¸¿®A1µ´≤ª∞¸¿®B1µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™a° R£¨∫Ø ˝f£®x£©=|x+ ![]() ©Åa|+a‘⁄«¯º‰[1£¨4]…œµƒ◊Ó¥Û÷µ «5£¨‘Úaµƒ»°÷µ∑∂Œß « £Æ
©Åa|+a‘⁄«¯º‰[1£¨4]…œµƒ◊Ó¥Û÷µ «5£¨‘Úaµƒ»°÷µ∑∂Œß « £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨Ω«¶¡”ÎΩ«¶¬æ˘“‘OxŒ™ º±þ£¨À¸√«µƒ÷’±þπÿ”⁄y÷·∂‘≥∆£¨»Ùsin¶¡= ![]() £¨‘Úcos£®¶¡©Å¶¬£©= £Æ
£¨‘Úcos£®¶¡©Å¶¬£©= £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=excosx©Åx£Æ£®13∑÷£©
£®1£©«Û«˙œþy=f£®x£©‘⁄µ„£®0£¨f£®0£©£©¥¶µƒ«–œþ∑Ω≥ãª
£®2£©«Û∫Ø ˝f£®x£©‘⁄«¯º‰[0£¨ ![]() ]…œµƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
]…œµƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨«“¬˙◊„£∫£¨
£¨«“¬˙◊„£∫£¨![]() £¨
£¨
(1)°¢«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £ª
£ª
£®2£©°¢»Ù≤ªµ» Ω![]() ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß°£
µƒ»°÷µ∑∂Œß°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2013ƒÍ1‘¬£¨±±æ©æ≠¿˙¡À59ƒÍ¿¥ŒÌˆ≤ÃÏ∆¯◊Ó∂ýµƒ“ª∏ˆ‘¬£Ææð∆¯œÛæ÷Õ≥º∆£¨±±æ© –2013ƒÍ1‘¬1»’÷¡1‘¬30»’’‚30ÃÏ¿Ô”–26ÃÏ≥ˆœ÷ŒÌˆ≤ÃÏ∆¯£¨°∂ª∑æ≥ø’∆¯÷ ¡ø÷∏ ˝(AQI)ºº ıπÊ∂®( ‘––)°∑»Á±Ì1£∫
±Ì1°°ø’∆¯÷ ¡ø÷∏ ˝AQI∑÷◊ȱÌ
AQI÷∏ ˝M | 0°´50 | 51°´100 | 101°´150 | 151°´200 | 201°´300 | >300 |
º∂± | ¢Ò | ¢Ú | ¢Û | ¢Ù | ¢ı | ¢ˆ |
◊¥øˆ | ”≈ | ¡º | «·∂»Œ€»æ | ÷–∂»Œ€»æ | ÷ÿ∂»Œ€»æ | —œ÷ÿŒ€»æ |
±Ì2 «ƒ≥∆¯œÛπ€≤‚µ„º«¬ºµƒ¡¨–¯4ÃÏ¿ÔAQI÷∏ ˝M”ε±Ãϵƒø’∆¯ÀÆ∆Ωø…º˚∂»y(km)µƒ«Èøˆ£¨±Ì3 «ƒ≥∆¯œÛπ€≤‚µ„º«¬ºµƒ±±æ© –2013ƒÍ1‘¬1»’÷¡1‘¬30»’µƒAQI÷∏ ˝∆µ ˝∑÷≤º±Ì£Æ
±Ì2°°AQI÷∏ ˝M”ε±Ãϵƒø’∆¯ÀÆ∆Ωø…º˚∂»y(km)µƒ«Èøˆ
AQI÷∏ ˝M | 900 | 700 | 300 | 100 |
ø’∆¯ÀÆ∆Ωø…º˚∂»y(km) | 0.5 | 3.5 | 6.5 | 9.5 |
±Ì3°°±±æ© –2013ƒÍ1‘¬1»’÷¡1‘¬30»’AQI÷∏ ˝∆µ ˝∑÷≤º±Ì
AQI÷∏ ˝M | [0£¨200) | [200£¨400) | [400£¨600) | [600£¨800) | [800£¨1000] |
∆µ ˝ | 3 | 6 | 12 | 6 | 3 |
£®1£©…Ëx£Ω![]() £¨∏˘æð±Ì2µƒ ˝æ𣨫Û≥ˆyπÿ”⁄xµƒœþ–‘ªÿπÈ∑Ω≥ãÆ
£¨∏˘æð±Ì2µƒ ˝æ𣨫Û≥ˆyπÿ”⁄xµƒœþ–‘ªÿπÈ∑Ω≥ãÆ
(≤Œøºπ´ Ω£∫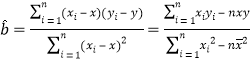 £¨
£¨![]() £Æ)
£Æ)
(2)–°Õı‘⁄±±æ©ø™¡À“ªº“œ¥≥µµÍ£¨æ≠–°ÕıÕ≥º∆£∫µ±AQI÷∏ ˝µÕ”⁄200 ±£¨œ¥≥µµÍ∆Ωæ˘√øÃÏø˜À‘º2000‘™£ªµ±AQI÷∏ ˝‘⁄200÷¡400 ±£¨œ¥≥µµÍ∆Ωæ˘√øÃÏ ’»Î‘º4000‘™£ªµ±AQI÷∏ ˝≤ªµÕ”⁄400 ±£¨œ¥≥µµÍ∆Ωæ˘√øÃÏ ’»Î‘º7000‘™£Æ
¢Ÿπ¿º∆–°Õıµƒœ¥≥µµÍ‘⁄2013ƒÍ1‘¬∑ð∆Ωæ˘√øÃϵƒ ’»Î£ª
¢⁄¥”AQI÷∏ ˝‘⁄[0£¨200)∫Õ[800£¨1000]ƒ⁄µƒ’‚6ÃÏ÷–≥È»°2ÃÏ£¨«Û’‚2Ãϵƒ ’»Î÷Æ∫Õ≤ªµÕ”⁄5000‘™µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫Ø ˝f£®x£©=ln£®x2©Å2x©Å8£©µƒµ•µ˜µð‘ˆ«¯º‰ «£® £©
A.£®©Å°Þ£¨©Å2£©
B.£®©Å°Þ£¨©Å1£©
C.£®1£¨+°Þ£©
D.£®4£¨+°Þ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨π˝Õ÷‘≤”“Ωπµ„
£¨π˝Õ÷‘≤”“Ωπµ„![]() ◊˜¡ΩÃıª•œý¥π÷±µƒœ“
◊˜¡ΩÃıª•œý¥π÷±µƒœ“![]() ”Î
”Î![]() £Æµ±÷±œþ
£Æµ±÷±œþ![]() –±¬ Œ™0 ±£¨
–±¬ Œ™0 ±£¨![]() £Æ
£Æ
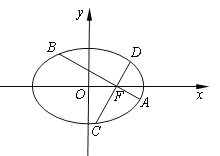
£®1£©«ÛÕ÷‘≤µƒ∑Ω≥ãª
£®2£©«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com