
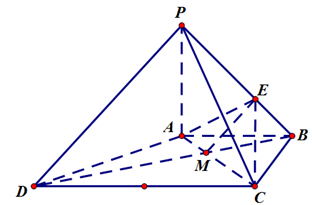
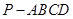 中,
中, ,底面
,底面 为梯形,
为梯形, ,
,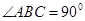 ,且
,且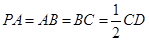 ,
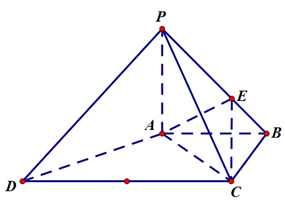
,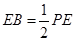 .
.
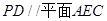 ;
; 的余弦值.
的余弦值.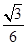 .
.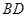 交
交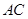 于
于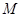 点,连结
点,连结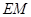 .由长度比例关系可知
.由长度比例关系可知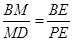 ,得到
,得到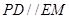 .再根据线面平行的判定得到
.再根据线面平行的判定得到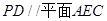 ;(2)方法一:采用空间向量法,以点
;(2)方法一:采用空间向量法,以点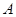 为坐标原点,
为坐标原点, 为
为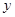 轴,垂直
轴,垂直 为
为 轴,
轴,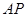 所在直线为
所在直线为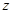 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设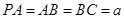 ,那么点
,那么点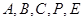 确定.再根据向量关系求出二面角的平面角的余弦值为
确定.再根据向量关系求出二面角的平面角的余弦值为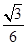 ;方法二:纯几何法,取
;方法二:纯几何法,取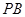 的中点
的中点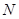 ,延长
,延长 交
交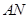 的延长线于点
的延长线于点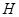 ,根据三角形相似关系可以得到二面角的平面角为
,根据三角形相似关系可以得到二面角的平面角为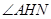 .
.
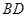 ,交
,交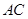 于点
于点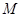 ,连结
,连结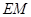 ,
, 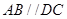 ,
,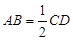 , ∴
, ∴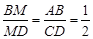
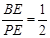 , ∴
, ∴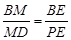
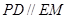
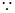
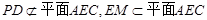
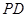 ∥平面
∥平面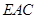
 为原点,
为原点, 所在直线分别为
所在直线分别为 轴、
轴、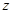 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
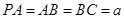 ,则
,则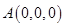 ,
,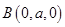 ,
,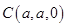 ,
,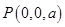 ,
,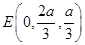 .
.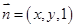 为平面
为平面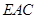 的一个法向量,
的一个法向量, ,
,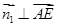 ,∴
,∴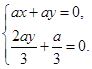 ,
,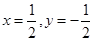 ,∴
,∴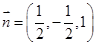 .
.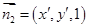 为平面
为平面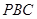 的一个法向量,则
的一个法向量,则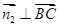 ,
,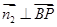 ,
,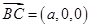 ,
,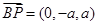 ,∴
,∴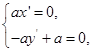 ,
,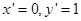 ,∴
,∴
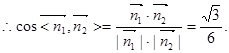
 的余弦值为
的余弦值为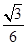 .
. 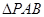 中,取
中,取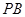 中点
中点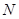 ,连结
,连结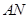 ,则
,则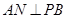

 ⊥面
⊥面 ,面
,面
 面
面 =
=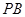 ,∴
,∴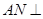 平面
平面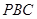 .
.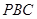 内,过
内,过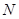 作
作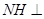 直线
直线 于
于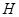 ,连结
,连结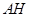 ,由
,由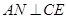 、
、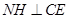 ,
,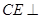 平面
平面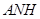 ,故
,故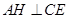 .
.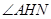 就是二面角
就是二面角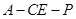 的平面角.
的平面角.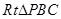 中,设
中,设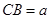 ,
,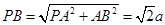 ,
,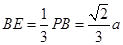 ,
,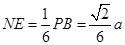 ,
,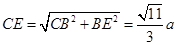 ,
, 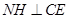 ,
,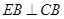 可知:
可知: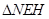 ∽
∽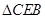 ,
,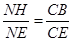 , 代入解得:
, 代入解得: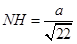 .
. 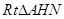 中,
中,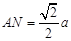 ,
,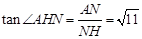 ,
,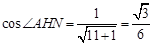 .
. 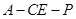 的余弦值为
的余弦值为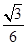 .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:不详 题型:解答题
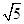 ,AB=AD=
,AB=AD=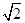 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).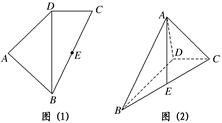
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
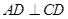 ,
,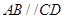 ,
,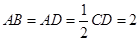 ,点M在线段EC上(除端点外)
,点M在线段EC上(除端点外)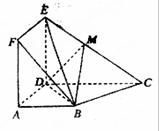
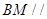 平面
平面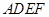 ;
;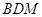 与平面ABF所成二面角为锐角,且该二面角的余弦值为
与平面ABF所成二面角为锐角,且该二面角的余弦值为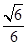 时,求三棱锥
时,求三棱锥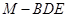 的体积
的体积查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com