
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,可得圆的直角坐标方程,求得A,B的直角坐标,即可得到直线AB的方程;
(Ⅱ)求得AB的距离和圆C和半径,求得圆C到直线AB的距离,由圆C上的点到直线AB的最大距离为d+r,运用三角形的面积公式,即可得到所求最大值.
解答 解:(Ⅰ)由ρ=2sinθ,可得:ρ2=2ρsinθ,所以x2+y2=2y,
圆的直角坐标方程为:x2+y2-2y=0(或x2+(y-1)2=1),
在直角坐标系中$A(4,0),B(3,\sqrt{3})$,
可得直线AB的方程为:$\sqrt{3}x+y-4\sqrt{3}=0$;
(Ⅱ)由(Ⅰ)可知圆心C(0,1),r=1,$|{AB}|=\sqrt{{{(4-3)}^2}+{{(0-\sqrt{3})}^2}}=2$,
圆心到直线AB的距离$d=\frac{{|{1-4\sqrt{3}}|}}{{\sqrt{4}}}=\frac{{4\sqrt{3}-1}}{2}$,
所以圆C上的点到直线AB的最大距离为d+r=$\frac{4\sqrt{3}-1}{2}$+1=$\frac{4\sqrt{3}+1}{2}$,
故△ABP面积的最大值为$S=\frac{1}{2}×2×\frac{{4\sqrt{3}+1}}{2}=\frac{{4\sqrt{3}+1}}{2}$.
点评 本题考查极坐标方程和直角坐标方程的互化,直线和圆方程的运用,注意运用圆上的点到直线的距离的最值,考查运算求解能力,考查化归与转化思想等.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
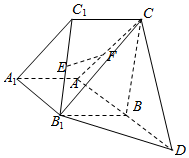 已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.
已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{4\sqrt{5}}{9}$ | C. | $\frac{10\sqrt{119}}{9}$ | D. | $\frac{4\sqrt{17}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+2)2+(y+1)2=5 | B. | (x+4)2+(y+2)2=20 | C. | (x-2)2+(y-1)2=5 | D. | (x-4)2+(y-2)2=20 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
已知直线 的方向向量
的方向向量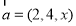 ,直线
,直线 的方向向量
的方向向量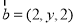 ,若
,若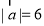 ,且
,且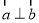 ,则
,则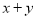 的值是( )
的值是( )
A.-3或1 B.3或-1 C.-3 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,2} | C. | {-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com