
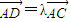 ,若CE⊥BD,则λ=( )
,若CE⊥BD,则λ=( )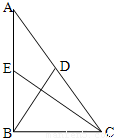
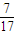
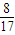
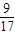
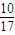
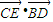 =0,运算求得λ的值.
=0,运算求得λ的值.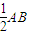 -BC,∴
-BC,∴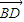 =
=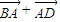 =
=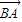 +λ
+λ 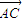 =(1-λ)
=(1-λ) 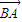 +λ
+λ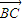 .
.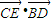 =0,即
=0,即  (1-λ) AB2-λ BC2=0,8(1-λ)-9λ=0,
(1-λ) AB2-λ BC2=0,8(1-λ)-9λ=0,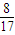 ,
,

科目:高中数学 来源: 题型:
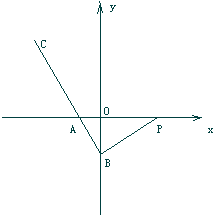 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使| BC |
| BA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•武昌区模拟)如图,已知直角三角形△ABC的三边CB,BA,AC的长度成等差数列,点E为直角边AB的中点,点D在斜边AC上,且
(2012•武昌区模拟)如图,已知直角三角形△ABC的三边CB,BA,AC的长度成等差数列,点E为直角边AB的中点,点D在斜边AC上,且| AD |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
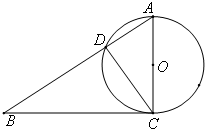 (2012•惠州一模)(几何证明选讲选做题)如图,已知直角三角形ABC中,∠ACB=90°,BC=4,AC=3,以AC为直径作圆O交AB于D,则CD=
(2012•惠州一模)(几何证明选讲选做题)如图,已知直角三角形ABC中,∠ACB=90°,BC=4,AC=3,以AC为直径作圆O交AB于D,则CD=| 12 |
| 5 |
| 12 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市武昌区高三5月调研考试文科数学试卷(解析版) 题型:选择题
如图,已知直角三角形 的三边
的三边 的长度成等差数列,点
的长度成等差数列,点 为直角边AB的中点,点D在斜边AC上,且
为直角边AB的中点,点D在斜边AC上,且 ,若
,若 ,则
,则

A.  B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com