
分析 (1)由$\left\{{\begin{array}{l}{{x_0}=ax}\\{{y_0}=by}\end{array}}\right.$,代入椭圆方程即可求得椭圆C上的点M的“伴随点”N的轨迹方程;
(2)由题意,求得椭圆的方程,根据向量的坐标运算,即可求得$\overrightarrow{OM}•\overrightarrow{ON}$的取值范围;
(3)求得椭圆方程,设方程为y=kx+m,代入椭圆方程,利用韦达定理,根据向量数量积的坐标求得3+4k2=2m2,弦长公式及点到直线的距离公式,即可求得△OAB的面积,直线l的斜率不存在时,设方程为x=m,代入椭圆方程,即可求得△OAB的面积.
解答 解:(1)设N(x,y)由题意 $\left\{{\begin{array}{l}{x=\frac{x_0}{a}}\\{y=\frac{y_0}{b}}\end{array}}\right.$,则$\left\{{\begin{array}{l}{{x_0}=ax}\\{{y_0}=by}\end{array}}\right.$,
又$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1(a>b>0)$,
∴$\frac{{{{(ax)}^2}}}{a^2}+\frac{{{{(by)}^2}}}{b^2}=1(a>b>0)$,
从而得x2+y2=1…(3分)
(2)由$\frac{1}{2}=\frac{1}{a}$,得a=2.又$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$,得$b=\sqrt{3}$.…(5分)
∵点M(x0,y0)在椭圆上,$\frac{x_0^2}{4}+\frac{y_0^2}{3}=1$,$y_0^2=3-\frac{3}{4}x_0^2$,且$0≤x_0^2≤4$,
$\overrightarrow{OM}$•$\overrightarrow{ON}$=(x0,y0)($\frac{{x}_{0}}{2}$,$\frac{{y}_{0}}{\sqrt{3}}$)=$\frac{{x}_{0}^{2}}{2}$+$\frac{{y}_{0}^{2}}{\sqrt{3}}$=$\frac{2-\sqrt{3}}{4}$x02+$\sqrt{3}$,
由于$\frac{{2-\sqrt{3}}}{4}>0$,$\overrightarrow{OM}•\overrightarrow{ON}$的取值范围是[$\sqrt{3}$,2](8分)
(3)设A(x1,y1),B(x2,y2),则$P({\frac{x_1}{2},\frac{y_1}{{\sqrt{3}}}}),\;Q({\frac{x_2}{2},\frac{y_2}{{\sqrt{3}}}})$;
1)当直线l的斜率存在时,设方程为y=kx+m,由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,
得(3+4k2)x2+8kmx+4(m2-3)=0;
有$\left\{\begin{array}{l}△=48(3+4{k^2}-{m^2})>0\\{x_1}+{x_2}=\frac{-8km}{{3+4{k^2}}}\\{x_1}{x_2}=\frac{{4({m^2}-3)}}{{3+4{k^2}}}\end{array}\right.$①…(10分)
由以PQ为直径的圆经过坐标原点O可得:3x1x2+4y1y2=0;
整理得:$(3+4{k^2}){x_1}{x_2}+4mk({x_1}+{x_2})+4{m^2}=0$②
将①式代入②式得:3+4k2=2m2,…(12分)
3+4k2>0,则m2>0,△=48m2>0,
又点O到直线y=kx+m的距离$d=\frac{|m|}{{\sqrt{1+{k^2}}}}$,
丨AB丨=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$×$\frac{4\sqrt{3}\sqrt{3+4{k}^{2}-{m}^{2}}}{3+4{k}^{2}}$=$\sqrt{1+{k}^{2}}$×$\frac{4\sqrt{3}丨m丨}{3+4{k}^{2}}$,
∴${S_{△OAB}}=\frac{1}{2}|{AB}|d=\sqrt{3}$…(14分)
2)当直线l的斜率不存在时,设方程为x=m(-2<m<2)
联立椭圆方程得${y^2}=\frac{{3(4-{m^2})}}{4}$;代入3x1x2+4y1y2=0,得$3{m^2}-4•\frac{{3(4-{m^2})}}{4}=0$,
解得m2=2,从而${y^2}=\frac{3}{2}$,
S△OAB=$\frac{1}{2}$丨AB丨×d=$\frac{1}{2}$丨m丨丨y1-y2丨=$\sqrt{3}$,
综上:△OAB的面积是定值$\sqrt{3}$.…(16分)
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,向量数量积的坐标运算,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
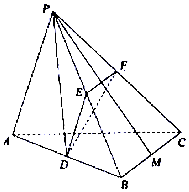 如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.
如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果l1∥α,l2∥α,则一定有l1∥l2 | B. | 如果l1⊥l2,l2⊥α,则一定有l1⊥α | ||
| C. | 如果l1⊥l2,l2⊥α,则一定有l1∥α | D. | 如果l1⊥α,l2∥α,则一定有l1⊥l2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com