
【题目】已知f(x)是定义在R上的偶函数,且在区间(﹣∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(﹣ ![]() ),则a的取值范围是( )
),则a的取值范围是( )
A.(﹣∞,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,+∞)
,+∞)
B.(﹣∞,﹣ ![]() )
)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣ ![]() ,﹣
,﹣ ![]() )
)
科目:高中数学 来源: 题型:
【题目】葫芦岛市交通局为了解机动车驾驶员对交通法规的知晓情况,对渤海、丰乐、安宁、天正四个社区做分层抽样调查.其中渤海社区有驾驶员96人.若在渤海、丰乐、安宁、天正四个社区抽取驾驶员的人数分别为12,21,25,43,则丰乐、安宁、天正三个社区驾驶员人数是多少( )
A.101
B.808
C.712
D.89
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 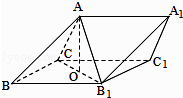
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0,
(1)求l2的方程,使得:①l2与l1平行,且过点(﹣1,3); ②l2与l1垂直,且l2与两坐标轴围成的三角形面积为4;
(2)直线l1与两坐标轴分别交于A、B 两点,求三角形OAB(O为坐标原点)内切圆及外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1 . 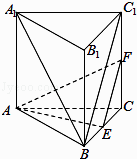
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com