
【题目】在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]()
![]() 平面
平面![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =2,
=2,![]() 是
是![]() 的中点.
的中点.
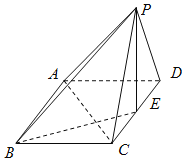
(Ⅰ)求证:![]()
![]()
![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】(Ⅰ)∵PD=PC,E为CD的中点,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,
∴PE⊥AC,(2分)
在Rt△BCE和Rt△ABC中,![]() ,∠ABC=∠BCE=90°,
,∠ABC=∠BCE=90°,
∴Rt△BCE∽Rt△ABC,
∴∠BAC=∠CBE,∠ACB=∠BEC,
∴∠EBC+∠ACB=∠CAB+∠ACB=90°,
∴BE⊥CA,(5分)
∵BE∩PE=E,
∴AC![]() 平面PBE,
平面PBE,
∴![]() .(6分)
.(6分)
(Ⅱ)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,连接AE,
,连接AE,
在Rt△EBC中,CE=1,BC=![]() ,∴BE=
,∴BE=![]() =
=![]() ,
,
在Rt△ADE中,AD=![]() ,DE=1,∴
,DE=1,∴![]() =
=![]() ,
,
在Rt△PEA中,PA=![]() =2, (8分)
=2, (8分)
在Rt△PEB中,PB=![]() =2,
=2,
∴![]() =
=![]() ,
,
∵![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部50名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 6 |
未参加演讲社团 | 6 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3,现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后随机投掷2枚正方体骰子,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,
(1)求点P(x,y)在直线y=x﹣1上的概率;
(2)求点P(x,y)满足y2<4x的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设AB=6,在线段AB上任取两点C、D(端点A、B除外),将线段AB分成三条线段AC、CD、DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称为事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称为事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数模拟的方法,来近似计算(2)中事件B的概率, 20组随机数如下:
组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
组别 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
(X和Y都是0~1之间的均匀随机数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() :
:![]() (
(![]() )分别交
)分别交![]() ,
,![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
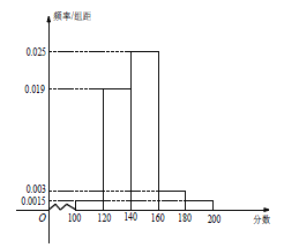
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com