下面的数组均由三个数组成,它们是:(1,2,3)、(2,4,6)、(3,8,11)、(4,16,20)、(5,32,37)…(an,bn,cn).
(1)数列{cn}的一个通项公式cn= (n∈N*);
(2)记Mn是数列{anbn}的前n项和,则M10= (用数字作答).
【答案】
分析:(1)分析每个数组的中间项,即b
n可得b
n=2
n,再分析每一个数组中第三项与第二项的关系,可得c
n=b
n+n,又由b
n=2
n,可得答案,
(2))由(1)可得c
n=2
n+n,用分组求和法可得M
10=(2
1+2
2+2
3+…+2
10)+(1+2+3+4+…+10),结合等差数列、等比数列的前n项和公式,计算可得答案.
解答:解:(1)分析每个数组的中间项,即b
n可得,b
1=2,b
2=4,b
3=8,b
4=16,…,易得b
n=2
n .
第一个数组中有c
1=b
1+1,
第二个数组中有c
2=b
2+2,
第三个数组中有c
3=b
3+3,
…
以此类推,可得c
n=b
n+n,又由b
n=2
n,则c
n=2
n+n,
故答案为 2
n+n.
(2)由(1)可得c
n=2
n+n,
∴M
10=c
1+c
2+c
3+…+c
10=(2
1+2
2+2
3+…+2
10)+(1+2+3+4+…+10)=
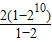
+
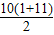
=2101,
故答案为2101.
点评:本题考查等比数列、等差数列的求和,涉及归纳推理的运用,解题的关键是运用归纳推理,得到c
n的关系式,属于中档题.

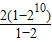 +
+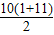 =2101,
=2101,

 阅读快车系列答案
阅读快车系列答案