考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)求出双曲线的a,b,c,焦点F
1(-5,0),F
2(5,0),运用双曲线的定义可得|AM|+|AF
2|=|AM|+|AF
1|-8,连接MF
1,由两点间线段最短,即可得到最小值;
(2)讨论当|n|≤
时,M在双曲线上或开口之内,连接MF
1,当|n|>
时,M在双曲线的开口之外,连接MF
2,
由两点间最短,即可得到最小值.
解答:
解:(1)双曲线
-
=1的a=4,b=3,
c=
=5,F
1(-5,0),F
2(5,0),
则由定义可得|AF
1|-|AF
2|=2a=8,
|AM|+|AF
2|=|AM|+|AF
1|-8,
连接MF
1,则|AM|+|AF
1|-8≥|MF
1|-8
=
-8=
-8,
当且仅当M,A,F
1共线时,取得最小值,
且为
-8;
(2)当|n|≤
时,M在双曲线上或开口之内,
则连接MF
1,则|AM|+|AF
1|-8≥|MF
1|-8
=
-8,
当且仅当M,A,F
1共线时,取得最小值,且为
-8;
当|n|>
时,M在双曲线的开口之外,连接MF
2,
则|AM|+|AF
2|≥|MF
2|=|n|.
当且仅当M,A,F
2共线时,取得最小值,且为|n|.
综上可得,当|n|≤
时,|AM|+|AF
2|的最小值为
-8;
当|n|>
时,最小值为|n|.
点评:本题考查双曲线的定义、方程和性质,考查两点之间线段最短,考查两点的距离公式,考查运算能力,属于中档题和易错题.



 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
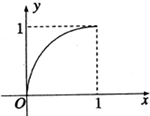 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: