
分析 (1)根据函数的奇偶性可得f(-x)+g(-x)=2-x+1,通过联立求解可得出函数的解析式;
(2)φ(x)是R上以2为正周期的周期函数,可得2016也为函数的周期,x-2016∈[-1,0],可得$φ(x)=φ(x-2016)=f(x-2016)={2^{x-2016}}+\frac{1}{{{2^{x-2016}}}}$,利用定义法判断函数的单调性即可;
(3)利用换元法t=g(x)在x∈[1,2]单调递增,得出t的范围$\frac{3}{2}≤t≤\frac{15}{4}$,不等式可整理为$m≥-\frac{{{t^2}+2}}{2t}$对于$t∈[{\frac{3}{2},\frac{15}{4}}]$恒成立,只需求出右式的最大值即可.
解答 解:(1)f(x)+g(x)=2x+1①,
因为f(x)是偶函数,g(x)是奇函数
所以有f(-x)+g(-x)=2-x+1,即f(x)-g(x)=2-x+1②
∵f(x),g(x)定义在实数集R上,
由①和②解得,$f(x)=\frac{{{2^{x+1}}+{2^{-x+1}}}}{2}={2^x}+\frac{1}{2^x}$,$g(x)=\frac{{{2^{x+1}}-{2^{-x+1}}}}{2}={2^x}-\frac{1}{2^x}$.
(2)φ(x)是R上以2为正周期的周期函数,所以当x∈[2015,2016]时,x-2016∈[-1,0],$φ(x)=φ(x-2016)=f(x-2016)={2^{x-2016}}+\frac{1}{{{2^{x-2016}}}}$,即φ(x)在闭区间[2015,2016]上的表达式为$φ(x)={2^{x-2016}}+\frac{1}{{{2^{x-2016}}}}$.
下面证明φ(x)在闭区间[2015,2016]上递减:$φ(x)={2^{x-2016}}+\frac{1}{{{2^{x-2016}}}}≥2$,当且仅当2x-2016=1,即x=2016时等号成立.
对于任意2015≤x1<x2≤2016,
$f({x_1})-f({x_2})={2^{{x_1}-2016}}+\frac{1}{{{2^{{x_1}-2016}}}}-{2^{{x_2}-2016}}-\frac{1}{{{2^{{x_2}-2016}}}}=({2^{{x_1}-{x_2}}}-1)({2^{{x_2}-2016}}-\frac{1}{{{2^{{x_1}-2016}}}})$,
因为2015≤x1<x2≤2016,所以${2^{{x_1}-{x_2}}}<1,{2^{{x_1}-{x_2}}}-1<0$,${2^{{x_2}-2016}}≤{2^0}=1$,${2^{{x_1}-2016}}<{2^0}=1$,$\frac{1}{{{2^{{x_1}-2016}}}}>1$,${2^{{x_2}-2016}}-{2^{2016-{x_1}}}<0$,
从而φ(x1)-φ(x2)>0,
所以当2015≤x1<x2≤2016时,φ(x)递减.
(3)∵t=g(x)在x∈[1,2]单调递增,∴$\frac{3}{2}≤t≤\frac{15}{4}$.
∴h(t)=t2+2mt+m2-m+1≥m2-m-1对于$t∈[{\frac{3}{2},\frac{15}{4}}]$恒成立,
∴$m≥-\frac{{{t^2}+2}}{2t}$对于$t∈[{\frac{3}{2},\frac{15}{4}}]$恒成立,
令$k(t)=-\frac{{{t^2}+2}}{2t}$,则$\frac{{{t^2}+2}}{2t}=\frac{t}{2}+\frac{1}{t}≥\sqrt{2}$,当且仅当$t=\sqrt{2}$时,等号成立,且$\sqrt{2}<\frac{3}{2}$所以在区间$t∈[{\frac{3}{2},\frac{15}{4}}]$上$k(t)=-\frac{{{t^2}+2}}{2t}$单调递减,
∴$k{(t)_{max}}=k(\frac{3}{2})=-\frac{17}{12}$,
∴$m≥-\frac{17}{12}$为m的取值范围.
点评 本题综合性强,考查了函数的奇偶性,周期性,单调性和恒成立问题的转化,换元法的应用.属于难度较大的题型.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-4,0} | B. | [-4,0] | C. | (-∞,0] | D. | (-∞,-4]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{r+1}{n+1}C_{n-1}^{r-1}$ | B. | $\frac{n+1}{r+1}C_{n-1}^{r-1}$ | C. | $\frac{r}{n}C_{n-1}^{r-1}$ | D. | $\frac{n}{r}C_{n-1}^{r-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
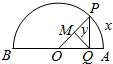 如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )| A. |  | B. | 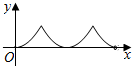 | C. |  | D. | 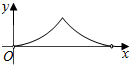 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com