
| A. | (-$\frac{1}{4}$,0) | B. | ($-\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($-\frac{1}{2}$,$-\frac{1}{4}$)∪($-\frac{1}{4}$,-$\frac{1}{8}$) | D. | (-$\frac{1}{2}$,$-\frac{1}{8}$) |
分析 做出f(x)的函数图象,令f(x)=t,根据图象得出方程f(x)=t的解的情况,得出t的范围,从而得出a的范围.
解答 解:作出f(x)的函数图象如图所示: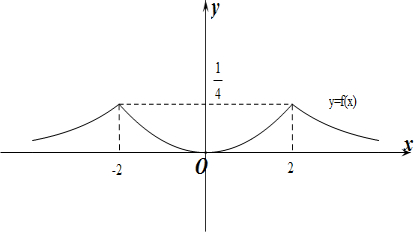
令f(x)=t,显然,当t=0时,方程f(x)=t只有一解x=0,
当0<t<$\frac{1}{4}$时,方程f(x)=t有四个解,
当t=$\frac{1}{4}$时,方程f(x)=t有两解,
当t<0或t>$\frac{1}{4}$时,方程f(x)=t无解.
∵关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有5个不同实数根,
∴关于t的方程t2+at+b=0,t∈R有两解,且一解为t1=0,另一解t2∈(0,$\frac{1}{4}$),
∴b=0,
∵t2+at=0的两解分别为t1=0,t2=-a,
∴0$<-a<\frac{1}{4}$,解得-$\frac{1}{4}$<a<0.
故选A.
点评 本题考查了函数零点的个数与函数图象的关系,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
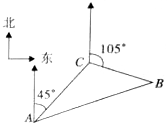 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=cos(2x$+\frac{π}{3}$) | B. | f(x)=-cos(2x-$\frac{π}{6}$) | C. | f(x)=-sin(2x+$\frac{π}{6}$) | D. | f(x)=sin(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 以2π为周期的偶函数 | B. | 以π为周期的偶函数 | ||
| C. | 以2π为周期的奇函数 | D. | 以π为周期的奇函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com