
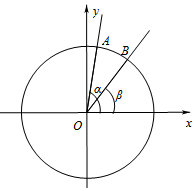
 如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.
如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.分析 (Ⅰ)根据三角函数的定义即可求tanα,利用同角三角函数基本关系式化简所求即可计算得解.
(Ⅱ)求出tanα,tanβ,即可求tan(α+β)的值,结合角的范围即可得解α+β的值.
解答 (本题满分12分)
解:(Ⅰ)由题意得,A($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$) …(1分)
∴tanα=7,…(3分)
∴$\frac{si{n}^{2}α+sinαcosα}{sinαcosα-6co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα}{tanα-6}$…(5分)
=$\frac{{7}^{2}+7}{7-6}$=56. …(6分)
(Ⅱ)由题意得,B($\frac{3}{5}$,$\frac{4}{5}$),tanβ=$\frac{4}{3}$,…(7分)
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$ …(8分)
=$\frac{7+\frac{4}{3}}{1-7×\frac{4}{3}}$ …(9分)
=-1. …(10分)
又∵α,β是锐角,
∴0<α+β<π,…(11分)
∴α+β=$\frac{3π}{4}$. …(12分)
点评 本题主要考查三角函数值的计算,要求熟练掌握相应的三角公式,属于基础题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
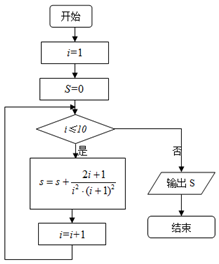
| A. | $\frac{1}{100}$ | B. | $\frac{1}{121}$ | C. | $\frac{99}{100}$ | D. | $\frac{120}{121}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个多面体的三视图和直观图如图所示,其中M,N,P分别是AB,SC,SD的中点.
一个多面体的三视图和直观图如图所示,其中M,N,P分别是AB,SC,SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| C. | 命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0” | |
| D. | △ABC中,A>B是sinA>sinB的充分必要条件. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com