
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线M的方程;
(2)过点F斜率为k的直线l与M相交于C,D两点,线段![]() 的垂直平分线
的垂直平分线![]() 与M相交于
与M相交于![]() 两点,点
两点,点![]() 分别为线段
分别为线段![]() 和
和![]() 的中点.
的中点.
①试用k表示点![]() 的坐标;
的坐标;
②若以线段![]() 为直径的圆过点C,求直线l的方程.
为直径的圆过点C,求直线l的方程.
【答案】(1)![]() (2)①
(2)①![]() ;
;![]() ②
②![]() ,或
,或![]()
【解析】
(1)根据题意可得![]() 且
且![]() ,解得
,解得![]() ,进而得出抛物线方程.
,进而得出抛物线方程.
(2)①点![]() 的坐标为
的坐标为![]() ,写出直线
,写出直线![]() 的方程为:
的方程为:![]() ,联立直线
,联立直线![]() 与抛物线
与抛物线![]() 的方程得
的方程得![]()
![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,则由韦达定理得
,则由韦达定理得![]() ,
,![]() ,进而得中点
,进而得中点![]() 的坐标,再写出线段
的坐标,再写出线段![]() 垂直平分线
垂直平分线![]() 的方程:
的方程:![]() ,联立它与抛物线方程,同理得线段
,联立它与抛物线方程,同理得线段![]() 中点
中点![]() 的坐标.
的坐标.
②根据题意得![]() ,
,![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,即
,即![]() ,分别由抛物线定义,弦长公式,两点之间得距离公式表示
,分别由抛物线定义,弦长公式,两点之间得距离公式表示![]() ,
,![]() ,
,![]() ,代入化简解得
,代入化简解得![]() ,进而得直线
,进而得直线![]() 的方程.
的方程.
解:(1)根据抛物线的定义和已知条件,得![]() ,故
,故![]() ,
,
由点Q在M上,可知![]() ,把
,把![]() 代入,得
代入,得![]() .
.
所以抛物线M的方程为:![]() .
.
(2)①由(1)可知点F的坐标为![]() ,所以直线l的方程为:
,所以直线l的方程为:![]() .
.
联立![]() 消去y得
消去y得![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以线段![]() 中点
中点![]() .
.
因为![]() 过点E且与l垂直,所以
过点E且与l垂直,所以![]() 的方程为:
的方程为:![]()
联立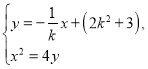 消去y,得
消去y,得![]() ,
,![]() 显然成立.
显然成立.
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以线段![]() 中点
中点![]()
②因为以线段![]() 为直径的圆过点C,所以
为直径的圆过点C,所以![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() .
.
根据抛物线定义,得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
所以,由![]() ,
,
得![]() ,
,
解方程得![]() ,所以直线l的方程为
,所以直线l的方程为![]() ,或
,或![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某段城铁线路上依次有![]() 、
、![]() 、
、![]() 三站,
三站,![]() ,
,![]() ,在列车运行时刻表上,规定列车
,在列车运行时刻表上,规定列车![]() 时整从
时整从![]() 站出发,
站出发,![]() 时
时![]() 分到达
分到达![]() 站并停车
站并停车![]() ,
,![]() 时
时![]() 分到达
分到达![]() 站,在实际运行时,假设列车从
站,在实际运行时,假设列车从![]() 站正点出发,在
站正点出发,在![]() 站停留
站停留![]() ,并在行驶时以同一速度
,并在行驶时以同一速度![]() 匀速行驶,列车从
匀速行驶,列车从![]() 站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在![]() 、
、![]() 两站的运行误差;
两站的运行误差;
(2)若要求列车在![]() 、
、![]() 两站的运行误差之和不超过
两站的运行误差之和不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在气象台![]() 正南方向
正南方向![]() 处有一台风中心,它以
处有一台风中心,它以![]() 的速度向北偏东
的速度向北偏东![]() 方向移动,距台风中心
方向移动,距台风中心![]() 以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台
以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台![]() 所在地将遭受台风影响?持续多长时间?(
所在地将遭受台风影响?持续多长时间?(![]() ,
,![]() ,结果精确到0.01)
,结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
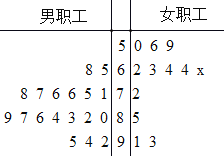
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比,药物释放完毕后,
成正比,药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).如图所示,根据图中提供的信息,回答下列问题:
为常数).如图所示,根据图中提供的信息,回答下列问题:
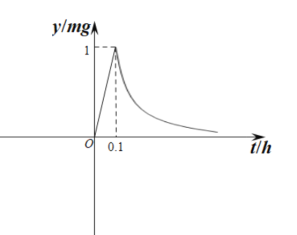
(1)从药物释放开始,每立方米空气中的含药量![]() 与时间
与时间![]() 之间的函数关系式为________;
之间的函数关系式为________;
(2)据测定,当空气中每立方米的含药量降低到![]() 以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com