设全集U=R,函数y=log
2(6-x-x
2)的定义域为A,函数y=
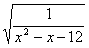
的定义域为B。
(1)求集合A与B;
(2)求A∩B,(C
UA)∪B
解:(1)函数y=log
2(6-x-x
2)要有意义需满足:6-x-x
2>0,解得-3<x<2,
∴A={x|-3<x<2}
函数

要有意义需满足x
2-x-12>0,解得x<-3或x>4
∴B={x|x<-3或x>4}。
(2)A∩B=
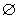
,C
UA={x|x≤-3或x≥2},
∴(C
UA)∪B={x|x≤-3或x≥2}。
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
设全集U=R,函数y=log
2(6-x-x
2)的定义域为A,函数
y=的定义域为B
(1)求集合A与B;
(2)求A∩B、(C
UA)∪B.
查看答案和解析>>
科目:高中数学
来源:
题型:
设全集U=R,函数
y=log(x+3)+的定义域为集合A,函数y=2
|x|的值域为集合B.求:
(I)A∪B;
(Ⅱ)(C
UA)∩B.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
设全集U=R,函数y=log2(6-x-x2)的定义域为A,函数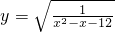 的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B
的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设全集U=R,函数
y=log(x+3)+的定义域为集合A,函数y=2
|x|的值域为集合B.求:
(I)A∪B;
(Ⅱ)(C
UA)∩B.
查看答案和解析>>

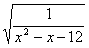 的定义域为B。
的定义域为B。