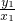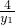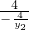练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知过抛物线C：y2=4x的焦点作直线与C分别相交于A、B两点，点M在抛物线的准线上．命题甲：直线BM与x轴平行；命题乙：直线AM过坐标原点．那么，命题甲是命题乙成立的


    1. A.
      充分不必要条件
    2. B.
      必要不充分条件
    3. C.
      充要条件
    4. D.
      既不充分也不必要条件
    C
    分析：设过焦点的直线方程为x=my+1与抛物线方程联立，表示出A、B两点坐标的关系，再利用斜率研究是否A，B，C三点共线 或BM与x轴是否平行．
    解答：设过焦点F（1，0）的直线方程为x=my+1 代入抛物线方程，消去x，并整理得，y2-4my-4=0，设A（x1，y1）B（x2，y2），则y1y2=-4，继而两边平方，16=16x1x2，∴x1x2=1
    若直线BM与x轴平行，则B（-1，y2），此时kOA====y2=kOM，k，o，m三点共线，即直线AM过坐标原点．
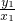    反之，若直线AM过坐标原点，则直线AM的方程为 y=x，，与抛物线准线方程x=-1联立得B的纵坐标为y=-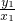=-=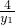y2，所以直线BM与x轴平行
    综上所述甲是乙成立的充要条件
    故选C
    点评：本题考查抛物线焦点弦的性质，直线和抛物线位置关系，及充要条件的判断．本题中设过焦点F（1，0）的直线方程为x=my+1，可以避免对斜率是否存在的讨论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知过抛物线C：y2=4x的焦点作直线与C分别相交于A、B两点，点M在抛物线的准线上．命题甲：直线BM与x轴平行；命题乙：直线AM过坐标原点．那么，命题甲是命题乙成立的（　　）
    A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知过抛物线C：y2=2px（p＞0）焦点F的直线l和y轴正半轴交于点A，并且l与C在第一象限内的交点M恰好为A、F的中点，则直线的斜率k=
    -2
    		2
    -2
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•上海二模）已知过抛物线C：y2=2px（p＞0）焦点F的直线l和y轴正半轴交于点A，并且l与C在第一象限内的交点M恰好为线段AF的中点，则直线l的倾斜角为
    π-arctan2
    		2
    π-arctan2
    		2
    ．（结果用反三角函数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知过抛物线C：y2=2px（p＞0）的焦点，斜率为2
    		2
    的直线交抛物线于A(x1，y2)，B(x2，y2)，且|AB|=
    9
    2

    （1）求该抛物线的方程；
    （2）在抛物线C上求一点D，使得点D直线y=x+3的距离最短．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市静安、杨浦、青浦、宝山区高考数学二模试卷（理科）（解析版） 题型：解答题

    已知过抛物线C：y2=2px（p＞0）焦点F的直线l和y轴正半轴交于点A，并且l与C在第一象限内的交点M恰好为线段AF的中点，则直线l的倾斜角为    ．（结果用反三角函数值表示）

    查看答案和解析>>

    同步练习册答案