
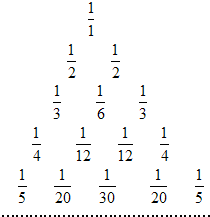 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
分析 根据“牛顿调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,就得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字.
解答 解:将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,就得到牛顿调和三角形.
∵杨晖三角形中第n(n≥3)行第3个数字是Cn-12,
则“牛顿调和三角形”第n(n≥3)行第3个数字是$\frac{1}{n{C}_{n-1}^{2}}$=$\frac{2}{n(n-1)(n-2)}$,
∴第2016第3个数$\frac{2}{2016×2015×2014}$=$\frac{1}{2016×2015×1007}$
故选:D.
点评 本题考查归纳推理,解题的关键是通过观察分析归纳各数的关系,考查学生的观察分析和归纳能力,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b<ab | B. | $\frac{b}{a}$+$\frac{a}{b}$>2 | C. | ab<b2 | D. | a2<b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com