练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】考虑某长方体的三个两两相邻的面上的三条对角线及体对角线（共四条线段），则正确的命题是（ ）

    A. 必有某三条线段不能组成一个三角形的三边

    B. 任何三条线段都可组成三角形，其每个内角都是锐角

    C. 任何三条线段都可组成三角形，其中必有一个是钝角三角形

    D. 任何三条线段都可组成三角形，其形状是“锐角的”或是“非锐角的”，随长方体的长、宽、高而变化，不能确定

    【答案】B

    【解析】

    设长方体的三度（即长、宽、高）为，，，则四条线段为，，，由三角形存在之判别定理（任两边之和大于第三边）及逆推法（两边平方）可知：任何三条线段都可构成三角形.然后，由余弦定理之推论（判别三角形之内角与的大小关系）及逆推法可知：每个三角形都是锐角三角形.（若从四条线段的几何意义入手是无法解本题的，应转化为代数问题）选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆.

    （1）若圆的切线在轴、轴上的截距相等，求切线方程；

    （2）从圆外一点向该圆引一条切线，切点为，且有（为坐标原点），求使取得最小值时点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，.

    （1）解关于的方程；

    （2）设，时，对任意，总有成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知分别是双曲线的左、右焦点，过点作垂直与轴的直线交双曲线于，两点，若为锐角三角形，则双曲线的离心率的取值范围是_______．

    【答案】

    【解析】

    根据双曲线的通径求得点的坐标，将三角形为锐角三角形，转化为，即，将表达式转化为含有离心率的不等式，解不等式求得离心率的取值范围.

    根据双曲线的通径可知，由于三角形为锐角三角形，结合双曲线的对称性可知，故，即，即，解得，故离心率的取值范围是.

    【点睛】

    本小题主要考查双曲线的离心率的取值范围的求法，考查双曲线的通径，考查双曲线的对称性，考查化归与转化的数学思想方法，属于中档题.本小题的主要突破口在将三角形为锐角三角形，转化为，利用列不等式，再将不等式转化为只含离心率的表达式，解不等式求得双曲线离心率的取值范围.

    【题型】填空题
    【结束】
    17

    【题目】已知命题：方程有两个不相等的实数根；命题：不等式的解集为.若或为真，为假，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0）的焦点为F，过F且斜率为的直线l与抛物线C交于A，B两点，B在x轴的上方，且点B的横坐标为4．

    （1）求抛物线C的标准方程；
    （2）设点P为抛物线C上异于A，B的点，直线PA与PB分别交抛物线C的准线于E，G两点，x轴与准线的交点为H，求证：HGHE为定值，并求出定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆M： 的离心率与双曲线的离心率互为倒数，且内切于圆。

    （1）求椭圆M的方程；

    （2）已知，是椭圆M的下焦点，在椭圆M上是否存在点P，使的周长最大？若存在，请求出周长的最大值，并求此时的面积；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数图象的一段，点M到l1、l2的距离分别为8千米和1千米，点N到l2的距离为10千米，以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy，设点P的横坐标为p．

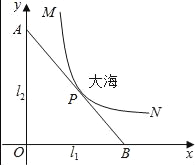
    （1）求曲线段MPN的函数关系式，并指出其定义域；

    （2）若某人从点O沿公路至点P观景，要使得沿折线OAP比沿折线OBP的路程更近，求p的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】梯形顶点在以为直径的圆上，米.

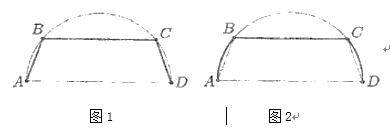
    （1）如图1，若电热丝由这三部分组成，在上每米可辐射1单位热量，在上每米可辐射2单位热量，请设计的长度，使得电热丝的总热量最大，并求总热量的最大值；

    （2）如图2，若电热丝由弧和弦这三部分组成，在弧上每米可辐射1单位热量，在弦上每米可辐射2单位热量，请设计的长度，使得电热丝辐射的总热量最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数的图象为C，则下列结论中正确的是（ ）

    A.图象C关于直线对称

    B.图象C关于点对称

    C.函数在区间内是增函数

    D.把函数的图象上点的横坐标缩短为原来的一半（纵坐标不变）可以得到图象C

    查看答案和解析>>

    同步练习册答案