练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四边形ABCD外切于，△ACB的内切圆与边AB、BC的切点分别为P、Q，，△ACD的内切圆与边CD、DA的切点分别为R、S. 求证：三条直线PQ、RS、AC共点或平行．

    【答案】见解析

    【解析】

    记、与AC的切点分别为、 由、分别是△ACB、△ACD的内切圆知

    又由四边形ABCD外切于知AB+AD=CB+CD．从而，

    这表明，点M与重合．

    若PQ∥AC，易知A、C两点关于直线BD对称，则RS∥AC.

    于是，PQ、RS、AC互相平行.

    若PQAC，则易知RSAC.

    如图，记直线PQ、RS分别与直线AC交于点N、

    对△ACB和截线PQN应用梅涅劳斯定理得

    结合BP=BQ，得 同理，

    这表明，点N与重合，即PQ、RS、AC三线共点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在2019年高考数学的全国Ⅲ卷中，文科和理科的选做题题目完全相同，第22题考查选修4-4：极坐标和参数方程；第23题考查选修4-5：不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式，在测试结束后，该校数学组教师对该校全体高三学生的选做题得分情况进行了统计，得到两题得分的列联表如下（已知每名学生只做了一道题）：

    选做22题

    选做23题

    合计

    文科人数

    50

    60

    理科人数

    40

    总计

    400

    （1）完善列联表中的数据，判断能否有的把握认为“选做题的选择”与“文、理科的科类”有关；

    （2）经统计，第23题得分为0的学生中，理科生占理科总人数的，文科生占文科总人数的，在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导，并在辅导后随机抽取2名学生进行测试，求被抽中进行测试的2名学生均为理科生的概率.

    附：，其中.

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，。

    （1）求的单调区间；

    （2）讨论零点的个数；

    （3）当时，设恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】大型综艺节目《最强大脑》中，有一个游戏叫做盲拧魔方，就是玩家先观察魔方状态并进行记忆，记住后蒙住眼睛快速还原魔方，盲拧在外人看来很神奇，其实原理是十分简单的，要学会盲拧也是很容易的.为了解某市盲拧魔方爱好者的水平状况，某兴趣小组在全市范围内随机抽取了名魔方爱好者进行调查，得到的情况如表所示：

    用时（秒）

    男性人数

    15

    22

    14

    9

    女性人数

    5

    11

    17

    7

    附：，.

    0.100

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    （1）将用时低于秒的称为“熟练盲拧者”，不低于秒的称为“非熟练盲拧者”.请根据调查数据完成以下列联表，并判断是否有的把握认为是否为“熟练盲拧者”与性别有关？

    熟练盲拧者

    非熟练盲拧者

    男性

    女性

    （2）以这名盲拧魔方爱好者的用时不超过秒的频率，代替全市所有盲拧魔方爱好者的用时不超过秒的概率，每位盲拧魔方爱好者用时是否超过秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取名爱好者进行测试，其中用时不超过秒的人数最有可能（即概率最大）是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求所有正整数，使得给定序列，，中的每一项都是平方数。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列有关线性回归分析的四个命题：

    ①线性回归直线必过样本数据的中心点（）；

    ②回归直线就是散点图中经过样本数据点最多的那条直线；

    ③当相关性系数时，两个变量正相关；

    ④如果两个变量的相关性越强，则相关性系数就越接近于．

    其中真命题的个数为（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若对任意，恒成立，求的取值范围；

    （2）若函数有两个不同的零点，，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

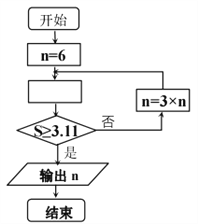
    【题目】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正边形求其面积，如图是其设计的一个程序框图，则框图中应填入、输出的值分别为（ ）

    （参考数据：）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系的极坐标方程为，直线l的参数方程为，（其中为参数）直线l与交于A，B两个不同的点．

    求倾斜角的取值范围；

    求线段AB中点P的轨迹的参数方程．

    查看答案和解析>>

    同步练习册答案