
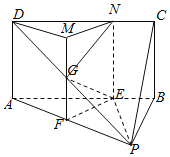
【题目】在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE︰EB=7︰2,点F、G分别为线段PA、PD的中点.

(1)求证:PE⊥平面ABCD;
(2)若平面EFG将四棱锥P-ABCD分成左右两部分,求这两部分的体积之比.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明PE⊥AB,利用平面PAB⊥平面ABCD,即可证明:PE⊥平面ABCD;
(2)平面EFG将四棱锥P﹣ABCD分成左右两部分,利用分割法求体积,即可求这两部分的体积之比.
证明:在等腰△APB中,得![]() ,
,
则由余弦定理可得,![]() ,∴
,∴![]() ,
,
∴PE2+BE2=4=PB2,∴PE⊥AB,
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PE⊥平面ABCD.
(2)解:设平面EFG与棱CD交于点N,连接EN,因为GF∥AD,所以GF∥平面ABCD,从而可得EN∥AD.
延长FG至点M,使GM=GF,连接DM,MN,则AFE﹣DMN为直三棱柱,
∵F到AE的距离为![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴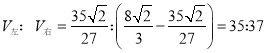 .
.


科目:高中数学 来源: 题型:
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
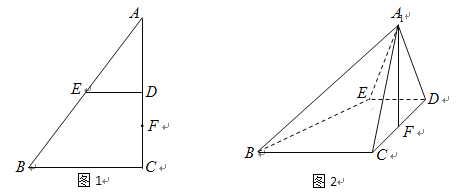
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1766年;人类已经发现的太阳系中的行星有金星、地球、火星、木星和土星.德国的一位中学教师戴维一提丢斯在研究了各行星离太阳的距离(单位:AU,AU是天文学中计量天体之间距离的一种单位)的排列规律后,预测在火星和木星之间应该还有一颗未被发现的行星存在,并按离太阳的距离从小到大列出了如下表所示的数据:
行星编号(x) | 1(金星) | 2(地球) | 3(火星) | 4( ) | 5(木星) | 6(土星) |
离太阳的距离(y) | 0.7 | 1.0 | 1.6 | 5.2 | 10.0 |
受他的启发,意大利天文学家皮亚齐于1801年终于发现了位于火星和木星之间的谷神星.
(1)为了描述行星离太阳的距离y与行星编号之间的关系,根据表中已有的数据画出散点图,并根据散点图的分布状况,从以下三种模型中选出你认为最符合实际的一种函数模型(直接给出结论即可);
①![]() ;②
;②![]() ;③
;③![]() .
.
(2)根据你的选择,依表中前几组数据求出函数解析式,并用剩下的数据检验模型的吻合情况;
(3)请用你求得的模型,计算谷神星离太阳的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地某高中2018年的高考考生人数是2015年高考考生人数的1.5倍.为了更好地对比该校考生的升学情况,统计了该校2015和2018年高考情况,得到如下饼图:

2018年与2015年比较,下列结论正确的是( )
A. 一本达线人数减少
B. 二本达线人数增加了0.5倍
C. 艺体达线人数相同
D. 不上线的人数有所增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com