
如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,. .
.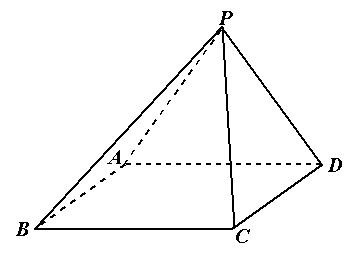
(1)求证:平面PAB丄平面PCD
(2)如果AB=BC=2,PB=PC=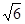 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积.
(1) 见解析 (2)
解析试题分析:(1)欲证平面 平面
平面 ,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证:
,只需证其中的一个平面经过另一平面的一条垂线即可,考虑到题设中所给的矩形以及面面垂直关系,易证: ,从而
,从而 平面
平面 ;
;
(2)作 ,垂足为
,垂足为 ,连结
,连结 ;可证
;可证 ≌
≌



 是
是 的中点,
的中点,
从而求得四棱锥的高 ,进一步求得四棱锥
,进一步求得四棱锥 的体积.
的体积.
试题解析:(Ⅰ)因为四棱锥 的底面是矩形,所以
的底面是矩形,所以 ,
,
又侧面 底面
底面 ,所以
,所以 .
.
又 ,即
,即 ,而
,而 ,所以
,所以 平面
平面 .
.
因为PAÌ平面PAB,所以平面PAB⊥平面PCD. 4分
(Ⅱ)如图,作PO⊥AD,垂足为O,则PO⊥平面ABCD.
连结OB,OC,则PO⊥OB,PO⊥OC.
因为PB=PC,所以Rt△POB≌Rt△POC,所以OB=OC.
依题意,ABCD是边长为2的正方形,由此知O是AD的中点. 7分
在Rt△OAB中,AB=2,OA=1,OB= .
.
在Rt△OAB中,PB= ,OB=
,OB= ,PO=1. 10分
,PO=1. 10分
故四棱锥P-ABCD的体积V= AB2·PO=
AB2·PO= .
.
考点:1、平面与平面垂直的判定与性质;2、棱锥的体积.


科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=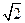 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.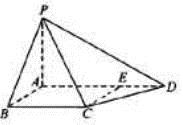
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.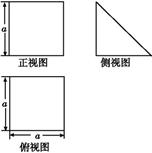

(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).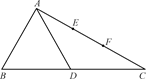
图①
图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=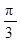 .
.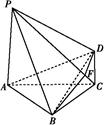
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.
BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱柱ABCD A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=
A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=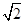 .
.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD A1B1D1的体积.
A1B1D1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥S ABC中,平面EFGH分别与BC,CA,AS,SB交于点E,F,G,H,且SA⊥平面EFGH,SA⊥AB,EF⊥FG.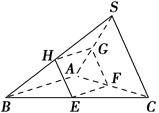
求证:(1)AB∥平面EFGH;
(2)GH∥EF;
(3)GH⊥平面SAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com