分析:(1)根据实数集A={x|a
1x=b
1,a
1b
1≠0},B={x|a
2x=b
2,a
2b
2≠0},根据等式的性质,易将A=B等价变形,易得A=B?
=,即A=B的充要条件是
=;
(2)可以先假定
==,然后判断A=B是否成立,然后再假设A=B成立,然后分A与B是否为空集两种情况进行分类讨论,即可得到结论.
解答:解:(1)∵
A={x|x=},
B={x|x=},
∴
A=B?=?=;(4分)
∴A=B的充要条件是
=;
(2)“
==”是“A=B”的充分不必要条件.(6分)
证明:充分性:
若x
0∈A,即x
0是方程a
1x
2+b
1x+c
1=0的解,则a
1x
02+b
1x
0+c
1=0,
而非零实数a
1,b
1,c
1和a
2,b
2,c
2满足
==,
设
===k≠0,则可得k(a
2x
02+b
2x
0+c
2)=0,
所以a
2x
02+b
2x
0+c
2=0,即x
0是方程a
2x
2+b
2x+c
2=0的解,即x
0∈B,
于是A⊆B.同理可证B⊆A,所以A=B(10分)
必要性不成立,反例:如A=B=?.(12分)
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,集合的相等,充要条件,根据等式的性质,结合集合相等的定义,对集合相等进行等价转化,是解答本题的关键.



 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案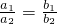 ;
;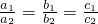 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程;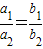 ;
;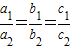 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程;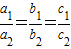 是A=B的什么条件?请给出说明过程.
是A=B的什么条件?请给出说明过程. ;
;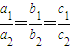 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程;