练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    从6名女生，4名男生中，按性别采用分层抽样的方法抽取5名学生组成课外小组，则不同
    的抽取方法种数为           
    A．B．C．D．学
    A
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题


    的展开式中的系数为
    A．4B．6
    C．10D．20

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    “上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所，其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体，为此，上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动．某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征，假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为，陶艺入选“中国馆·贵宾厅”的概率为．假定这四件作品是否入选相互没有影响．
    （1）求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
    （2）设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量，求的数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）
    在直角坐标系xOy中，已知圆心在第二象限、半径为2的圆C与直线y=x相切于
    坐标原点O.椭圆与圆C的一个交点到椭圆两焦点的距离之和为10。
    （1）求圆C的方程；
     （2）试探究圆C上是否存在异于原点的点Q，使Q到椭圆的右焦点F的距离等于线段
    OF的长，若存在求出Q的坐标；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    假设一个人从出生到死亡，在每个生日都测量身高，并作出这些数据散点图，则这些点将不会落在一条直线上，但在一段时间内的增长数据有时可以用线性回归来分析．下表是一位母亲给儿子作的成长记录：
    年龄／周岁
    		3
    		4
    		5
    		6
    		7
    		8
    		9
    身高／cm
    		90.8
    		97.6
    		104.2
    		110.9
    		115.6
    		122.0
    		128.5
    年龄／周岁
    		10
    		11
    		12
    		13
    		14
    		15
    		16
    身高／cm
    		134.2
    		140.8
    		147.6
    		154.2
    		160.9
    		167.6
    		173.0
    （1）作出这些数据的散点图；
    （2）求出这些数据的回归方程；
    （3）对于这个例子，你如何解释回归系数的含义？
    （4）用下一年的身高减去当年的身高，计算他每年身高的增长数，并计算他从3~16岁身高的年均增长数．
    （5）解释一下回归系数与每年平均增长的身高之间的联系．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知之间的一组数据如表所示，对于表中数据，现在给出如下拟合直线，则根据最小二乘法思想判断拟合程度最好的直线是（   ）

    		 2
    		 3
    		 4
    		 5
    		 6

    		 3
    		 4
    		 6
    		 8
    		 9
    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （满分13分）某项实验，在100次实验中成功率只有10％，进行技术改造后，又进行了100次实验，若要有97．5％以上的把握认为“技术改造效果明显”，实验的成功率最小应是多少？（设,的观测值为）
    （解答过程须列出列联表）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    甲、乙、丙三名射击运动员在某次测试中各射击20次，三人的测试成绩如下表
    甲的成绩
     环数
    		7
    		8
    		9
    		10
    频数
    		5
    		5
    		5
    		5

    乙的成绩
    环数
    		7
    		8
    		9
    		10
    频数
    		6
    		4
    		4
    		6

    丙的成绩
    环数
    		7
    		8
    		9
    		10
    频数
    		4
    		6
    		6
    		4

    分别表示甲、乙、丙三名运动员这次测试成绩的平均数，则的大小关系为 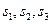             ；分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则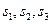的大小关系为              ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    对于变量与y随机抽取到的对数据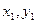（），（），…，（），利用相关系数来衡量两个变量之间线性相关系数的方法，样本相关系数的具体的计算公式为______________________,通常当大于_____时，我们认为两个变量存在着很强的线性相关关系.

    查看答案和解析>>

    同步练习册答案