
【题目】设函数f(x)=|2x+3|-|2x-a|,a∈R.
(1)若不等式f(x)≤-5的解集非空,求实数a的取值范围;
(2)若函数y=f(x)的图象关于点![]() 对称,求实数a的值.
对称,求实数a的值.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0.且a2,a5,a14分别是等比数列{bn}的b2,b3,b4.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有![]() 成立,求c1+c2+…+c2016的值.
成立,求c1+c2+…+c2016的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=2,数列{anan+1}是公比为q (q>0)的等比数列,则数列{an}的前2n项和S2n=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
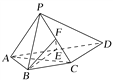
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
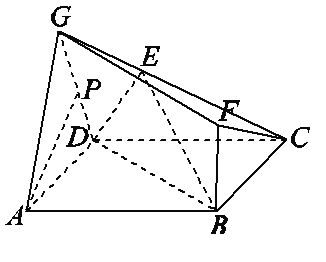
【题目】如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,BF⊥平面ABCD,∠GDC=90°,点E是线段GC上除两端点外的一点,若点P为线段GD的中点.
(Ⅰ)求证:AP⊥平面GCD;
(Ⅱ)求证:平面ADG∥平面FBC;
(Ⅲ)若AP∥平面BDE,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点![]() ,抛物线上的点
,抛物线上的点![]() ,过点B作直线AP的垂线,垂足为Q.
,过点B作直线AP的垂线,垂足为Q.
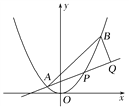
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com