
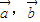 是两个非零向量,且
是两个非零向量,且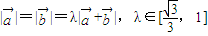 ,则
,则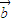 与
与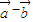 的夹角的取值范围是 .
的夹角的取值范围是 . 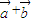 |=1,则|
|=1,则|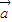 |=|
|=|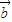 |=λ.令
|=λ.令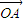 =
=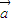 ,
,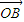 =
=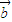 ,以OA、OB为临边作平行四边形OACB,则平行四边形OACB
,以OA、OB为临边作平行四边形OACB,则平行四边形OACB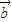 与
与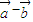 的夹角,即
的夹角,即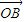 与
与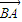 的夹角,等于π-θ,且0<θ<
的夹角,等于π-θ,且0<θ<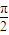 .△OAC中,由
.△OAC中,由 .再由
.再由 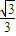 ≤λ≤1求得cos2θ的范围,从而求得θ的范围,即可得到
≤λ≤1求得cos2θ的范围,从而求得θ的范围,即可得到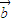 与
与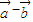 的
的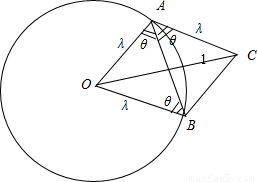 解:∵
解:∵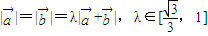 ,
,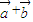 |=1,则|
|=1,则|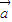 |=|
|=| |=λ.
|=λ.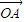 =
=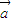 ,
,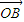 =
=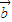 ,以OA、OB为邻边作平行四边形OACB,
,以OA、OB为邻边作平行四边形OACB,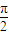 .
.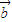 与
与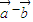 的夹角,即
的夹角,即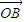 与
与 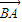 的夹角,
的夹角,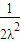 .
.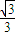 ≤λ≤1,可得
≤λ≤1,可得  ≤
≤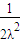 ≤
≤ ,∴-
,∴- ≤cos2θ≤
≤cos2θ≤ ,∴
,∴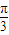 <2θ≤
<2θ≤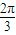 ,∴
,∴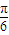 <θ≤
<θ≤ ,
, ≤π-θ<
≤π-θ<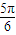 ,即
,即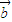 与
与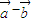 的夹角π-θ的取值范围是[
的夹角π-θ的取值范围是[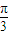 ,
,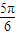 ).
).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com