
【题目】设![]() 是定义在
是定义在![]() 上的奇函数,且对任意
上的奇函数,且对任意![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,试比较
,试比较![]() 与
与![]() 的大小关系;
的大小关系;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由![]() ,所以
,所以![]() ,根据
,根据![]() 和函数的奇偶性,即可比较
和函数的奇偶性,即可比较![]() 与
与![]() 的大小关系;(2)由(1)知
的大小关系;(2)由(1)知![]() 为
为![]() 上的单调递增函数,把不等式的恒成立,转化为
上的单调递增函数,把不等式的恒成立,转化为![]() 对任意
对任意![]() 恒成立,构造新函数
恒成立,构造新函数![]() ,求的函数的最小值,即可求解实数
,求的函数的最小值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(1)因为![]() ,所以
,所以![]() ,由题意得:
,由题意得:
![]() ,所以
,所以![]() ,..................2分
,..................2分
又![]() 是定义在
是定义在![]() 上的奇函数,∴
上的奇函数,∴![]() ,
,
∴![]() ,即
,即![]() ...............5分
...............5分
(2)由(1)知![]() 为
为![]() 上的单调递增函数,..................6分
上的单调递增函数,..................6分
∵![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() ,...................8分
,...................8分
∴![]() ,∴
,∴![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 小于函数
小于函数![]() 的最小值.............10分
的最小值.............10分
令![]() ,则
,则![]() ,∴
,∴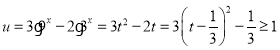 .............11分
.............11分
∴![]() ...................12分
...................12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】用反证法证明:“自然数a,b,c中恰有一个偶数”时正确的反设为 ( )
A. a,b,c都是偶数
B. a,b,c都是奇数
C. a,b,c中至少有两个偶数
D. a,b,c中都是奇数或至少有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.

(1)求证:DE∥平面ABC;
(2)求此空间几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下程序运行后的输出结果为
i=1
WHILE i<8
i=i+2
S=2*i+3
i=i–1
WEND
PRINT S
END
A. 17 B. 19 C. 21 D. 23
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组为调查当地居民的收入水平,他们对当地一个有5000人的社区随机抽取1000人,调查他们的月收入,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.
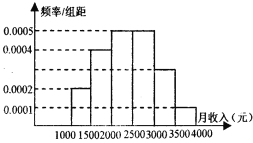
(Ⅰ)请你补上第五组顶部对应的纵轴数据,并估算该社区居民月收入在[3000,4000)的人数;
(Ⅱ)根据频率分布直方图估算样本数据的中位数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这1000人中用分层抽样方法抽出100人作进一步分析,则月收入在[2500,3000)的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列表述正确的是( )
①归纳推理是由特殊到一般的推理;②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;④分析法是一种间接证明法;
A. ②④ B. ①③ C. ①④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于程序框图的说法正确的是( )
①程序框图只有一个入口,也只有一个出口;
②程序框图的第一部分应有一条从入口到出口的路径通过它;
③程序框图的循环可以是无尽循环;
④程序框图中判断框内的条件是唯一的.
A. ①②③ B. ②③ C. ①④ D. ①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com