
 =(1,1),向量
=(1,1),向量 和向量
和向量 的夹角为
的夹角为 ,|
,| |=
|= ,
, •
• =-1.
=-1. ;
; 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量 =(cosA,
=(cosA,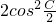 ),其中A、B、C为△ABC的内角a、b、c为三边,b2+ac=a2+c2,求|
),其中A、B、C为△ABC的内角a、b、c为三边,b2+ac=a2+c2,求| +
+ |的取值范围.
|的取值范围. =(x,y),由
=(x,y),由 =-1得x+y=-1,
=-1得x+y=-1, 和
和 的夹角为
的夹角为 ,,
,, =
= =-1,
=-1, |=1?x2+y2=1,
|=1?x2+y2=1, ,可解得
,可解得 =(-1,0)或(0,-1).
=(-1,0)或(0,-1). 与
与 =(1,0)的夹角为
=(1,0)的夹角为 知
知 =(0,-1),
=(0,-1), 得∠A+∠C=
得∠A+∠C= ,
,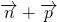 |2=
|2= =cos2A+cos2C=
=cos2A+cos2C= +
+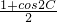

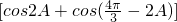 =
=
 =1+
=1+
 .
. ?
? <
<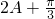 <
< ?
? ≤1+
≤1+
 <
< ,
,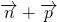 |的取值范围为[
|的取值范围为[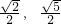 ).
).
 确定出
确定出 ,利用三角形的余弦定理求出∠B,利用向量模的坐标公式求出
,利用三角形的余弦定理求出∠B,利用向量模的坐标公式求出 ,利用三角函数的二倍角公式化简三角函数,利用整体思想求出三角函数的取值范围.
,利用三角函数的二倍角公式化简三角函数,利用整体思想求出三角函数的取值范围.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| 2 |
| m |
| n |
| n |
| n |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| n |
| p |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| n2+1 |
| a |
| b |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修4 2.5向量的应用练习卷(解析版) 题型:填空题
(2008海南、宁夏高考,理13)已知向量 =(0,-1,1),
=(0,-1,1),  =(4,1,0),|λ
=(4,1,0),|λ +
+ |=
|=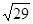 ,且λ>0,则λ=________________.
,且λ>0,则λ=________________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| 2 |
| m |
| n |
| n |
| n |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| n |
| p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com