
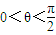 )则tanα=
)则tanα=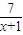 ,
,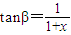 ,而tanθ=tan(α-β)=
,而tanθ=tan(α-β)=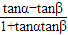 =
=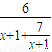 ,结合函数f(x)=x+1+
,结合函数f(x)=x+1+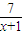 ,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=
,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=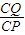 可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=
可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=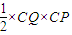 可求
可求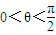 )
)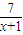 ,
,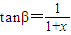
 =
=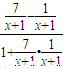 =
=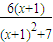 =
=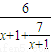
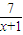 ,(x≥0)则f(x)在[0,
,(x≥0)则f(x)在[0,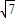 -1]单调递减在,
-1]单调递减在,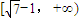 单调递增
单调递增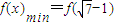 =
=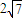 ,此时x+1=
,此时x+1=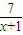 即
即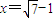 时,函数f(x)有最小值,tanθ最大也即θ最大
时,函数f(x)有最小值,tanθ最大也即θ最大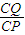 可得CQ=CP•tanβ=
可得CQ=CP•tanβ=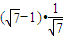 =
=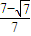
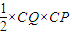 =
=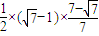 =
=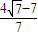
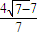

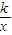 (k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键.
(k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键. 

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
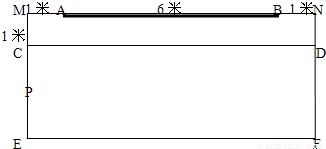
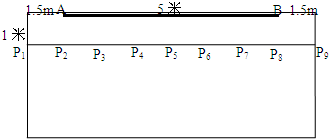 在宽为8米的教室前面有一个长为5米的黑板,距离黑板1米,间隔1米的学生Pi,i=1,2,…,9,如图,当视角∠APiB小于45°时,该学生处在教室黑板盲区,此类学生是
在宽为8米的教室前面有一个长为5米的黑板,距离黑板1米,间隔1米的学生Pi,i=1,2,…,9,如图,当视角∠APiB小于45°时,该学生处在教室黑板盲区,此类学生是查看答案和解析>>
科目:高中数学 来源: 题型:
4
| ||
| 7 |
4
| ||
| 7 |

查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源:2010年浙江省高考数学最新押题卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com