
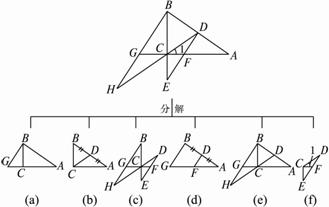
图1-3-16
求证:(1)GH·CE =DF·BC;
(2)DC2=DF·DE;
(3)CH·CD =GH·DE;
(4)GB∶BA =CH∶BH;
(5)CH·EF =BA·DF.
思路分析:(1)欲证原式,只需证![]() =
=![]() ,可在图(c)中由BH∥DE,容易得到
,可在图(c)中由BH∥DE,容易得到![]() =
=![]() ,
, ![]() =
=![]() ,利用中间比
,利用中间比![]() 代换即可,还可选中间比为
代换即可,还可选中间比为![]() .?
.?
(2)在图(f)中欲证原式,只需证![]() =
=![]() ,发现它们分别属于有公共角∠CDF的两个三角形:△DCF和△DEC.只需利用“直角三角形斜边中线的性质”及“同角的余角相等”证得∠1=∠E即可.?
,发现它们分别属于有公共角∠CDF的两个三角形:△DCF和△DEC.只需利用“直角三角形斜边中线的性质”及“同角的余角相等”证得∠1=∠E即可.?
(3)欲证原式,只需证![]() =
=![]() .可直接证明△CGH∽△ECD(图(c)也可利用相似三角形的传递性(△CGH∽△CFD,△CFD∽△ECD)来实现.?
.可直接证明△CGH∽△ECD(图(c)也可利用相似三角形的传递性(△CGH∽△CFD,△CFD∽△ECD)来实现.?
(4)所要证的比例式中的四条线段既不满足“三角形一边的平行线”条件,也不构成相似三角形的对应边,但在图(e)中发现,可通过△GBA∽△GCB得到中间比![]() =
=![]() .证明
.证明![]() =
=![]() 可由证明△GCH∽△CBH来实现.?
可由证明△GCH∽△CBH来实现.?
(5)欲证原式,只需证![]() =
=![]() .但无法由证明三角形相似实现,经过观察图(d),
.但无法由证明三角形相似实现,经过观察图(d), ![]() ,而
,而![]() =
=![]() =
=![]() ,可与图(c)联系起来,得到
,可与图(c)联系起来,得到![]() (
(![]() )=
)=![]() ·(
·(![]() )=
)=
![]() (
(![]() )=
)=![]() (三角形一边平行线的性质),其中2CD =BA(图(b)).因此通过对线段的倍、分的转化(
(三角形一边平行线的性质),其中2CD =BA(图(b)).因此通过对线段的倍、分的转化(![]() ,2CD =BA),利用换中间比,换线段使问题得到解决.
,2CD =BA),利用换中间比,换线段使问题得到解决.
解:同上分析:?



 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
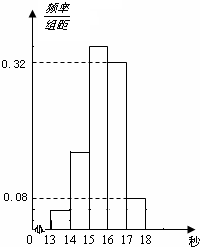 为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:
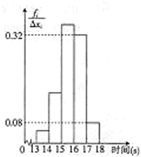 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:044

图1-3-16
求证:(1)GH·CE =DF·BC;?
(2)DC2=DF·DE;?
(3)CH·CD =GH·DE;?
(4)GB∶BA =CH∶BH;?
(5)CH·EF =BA·DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com