
已知:如图所示,在△ABC中,AB=AC,O是△ABC的外心,延长CA到P,再延长AB
到Q,使AP=BQ.求证:O,A,P,Q四点共圆.

证明 连接OA,OC,OP,OQ.
∵O是△ABC的外心,∴OA=OC.
∴∠OCP=∠OAC.
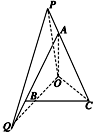 由于等腰三角形的外心在顶角的平分线上,
由于等腰三角形的外心在顶角的平分线上,
∴∠OAC=∠OAQ,
从而∠OCP=∠OAQ,
在△OCP和△OAQ中,
由已知CA=AB,AP=BQ,
∴CP=AQ.又OC=OA,
∠OCP=∠OAQ,
∴△OCP≌△OAQ,
∴∠CPO=∠AQO,
∴O,A,P,Q四点共圆.
证明 连接OA,OC,OP,OQ.
∵O是△ABC的外心,∴OA=OC.
∴∠OCP=∠OAC.
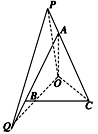 由于等腰三角形的外心在顶角的平分线上,
由于等腰三角形的外心在顶角的平分线上,
∴∠OAC=∠OAQ,
从而∠OCP=∠OAQ,
在△OCP和△OAQ中,
由已知CA=AB,AP=BQ,
∴CP=AQ.又OC=OA,
∠OCP=∠OAQ,
∴△OCP≌△OAQ,
∴∠CPO=∠AQO,
∴O,A,P,Q四点共圆.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013届甘肃省高二下学期第二次月考文科数学试卷(解析版) 题型:解答题
(12分)已知:如图所示,在△ABC中,D是BC的中点,F是BA延长线上的点,FD与AC交于点E.
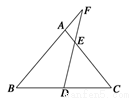
求证:AE·FB=EC·FA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com