
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求
时,求![]() 的值域和单调减区间;
的值域和单调减区间;
(2)若![]() 存在单调递增区间,求
存在单调递增区间,求![]() 的取值范围.
的取值范围.
【答案】(1)函数的值域为(-∞,0],f(x)的单调递减区间为[2,3)(2)a>![]()
【解析】
(1)当![]() 时,先求得
时,先求得![]() 的定义域,利用换元法,结合二次函数值域和对数函数值域的求法求得函数
的定义域,利用换元法,结合二次函数值域和对数函数值域的求法求得函数![]() 的值域;结合复合函数单调性同增异减求得函数
的值域;结合复合函数单调性同增异减求得函数![]() 的单调区间.
的单调区间.
(2)对![]() 分成
分成![]() 和
和![]() 两种情况进行分类讨论,根据复合函数单调性同增异减以及判别式,求得
两种情况进行分类讨论,根据复合函数单调性同增异减以及判别式,求得![]() 的取值范围.
的取值范围.
(1)当a=4时,f(x)=log4(-x2+4x-3)=log4[-(x-2)2+1],
设t=-x2+4x-3=-(x-2)2+1,
由-x2+4x-3>0,得x2-4x+3<0,得1<x<3,即函数的定义域为(1,3),
此时t=-(x-2)2+1∈(0,1],
则y=log4t≤log41,即函数的值域为(-∞,0],
要求f(x)的单调减区间,等价为求t=-(x-2)2+1的单调递减区间,
∵t=-(x-2)2+1的单调递减区间为[2,3),
∴f(x)的单调递减区间为[2,3).
(2)若f(x)存在单调递增区间,
则当a>1,则函数t=-x2+ax-3存在单调递增区间即可,则判别式△=a2-12>0得a>![]() 或a<
或a<![]() 舍,
舍,
当0<a<1,则函数t=-x2+ax-3存在单调递减区间即可,则判别式△=a2-12>0得a>![]() 或a<-
或a<-![]() ,此时a不成立,
,此时a不成立,
综上实数a的取值范围是a>![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲乙两位同学玩游戏,对于给定的实数![]() ,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把![]() 乘以2后再减去6;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去6;如果出现一个正面朝上,一个反面朝上,则把![]() 除以2后再加上6,这样就可得到一个新的实数
除以2后再加上6,这样就可得到一个新的实数![]() ,对实数
,对实数![]() 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数![]() ,当
,当![]() 时,甲获胜,否则乙获胜,若甲胜的概率为
时,甲获胜,否则乙获胜,若甲胜的概率为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组进行“野岛生存”实践活动,他们设置了![]() 个取水敞口箱.其中
个取水敞口箱.其中![]() 个采用
个采用![]() 种取水法,
种取水法,![]() 个采用
个采用![]() 种取水法.如图甲为
种取水法.如图甲为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图,图乙为
个水箱积取淡水量频率分布直方图,图乙为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图.
个水箱积取淡水量频率分布直方图.
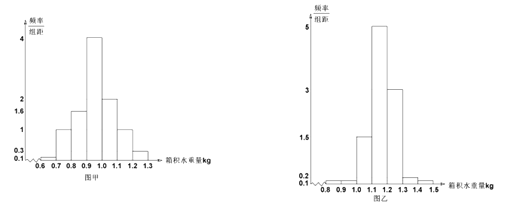
(1)设两种取水方法互不影响,设![]() 表示事件“
表示事件“![]() 法取水箱水量不低于
法取水箱水量不低于![]() ,
,![]() 法取水箱水量不低于
法取水箱水量不低于![]() ”,以样本估计总体,以频率分布直方图中的频率为概率,估计
”,以样本估计总体,以频率分布直方图中的频率为概率,估计![]() 的概率;
的概率;
(2)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为箱积水量与取水方法有关.
的把握认为箱积水量与取水方法有关.
箱积水量 | 箱积水量 | 箱数总计 | |
| |||
| |||
箱数总计 |
附:![]()
![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基因编辑婴儿“露露”和“娜娜”出生的消息成了全球瞩目的焦点,为了解学生对基因编辑婴儿的看法,某中学随机从该校一年级学生中抽取了100人进行调查,抽取的45女生中赞成基因编辑婴儿的占![]() ,而55名男生中有10人表示赞成基因编辑婴儿.
,而55名男生中有10人表示赞成基因编辑婴儿.
(1)完成![]() 列联表,并回答能否有90%的把握认为“对基因编辑婴儿是否赞成与性别有关”?
列联表,并回答能否有90%的把握认为“对基因编辑婴儿是否赞成与性别有关”?

(2)现从该校不赞成基因编辑婴儿的学生中,采用分层抽样的方法抽取7名学生,再从被抽取的7名学生中任取3人,记被抽取的3名学生女生的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为净化新安江水域的水质,市环保局于2017年底在新安江水域投入一些蒲草,这些蒲草在水中的蔓延速度越来越快,2018年二月底测得蒲草覆盖面积为![]() ,2018年三月底测得覆盖面积为
,2018年三月底测得覆盖面积为![]() ,蒲草覆盖面积
,蒲草覆盖面积![]() (单位:
(单位:![]() )与月份
)与月份![]() (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(Ⅰ)分别求出两个函数模型的解析式;
(Ⅱ)若市环保局在2017年年底投放了![]() 的蒲草,试判断哪个函数模型更合适?并说明理由;
的蒲草,试判断哪个函数模型更合适?并说明理由;
(Ⅲ)利用(Ⅱ)的结论,求蒲草覆盖面积达到![]() 的最小月份.
的最小月份.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 各条棱的长度均相等,
各条棱的长度均相等,![]() 为
为![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() ,当
,当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )

A. 在![]() 内总存在与平面
内总存在与平面![]() 平行的线段
平行的线段
B. 平面![]() 平面
平面![]()
C. 三棱锥![]() 的体积为定值
的体积为定值
D. ![]() 可能为直角三角形
可能为直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com