
【题目】已知函数![]() (m
(m![]() R)
R)
(1)当![]() 时,
时,
①求函数![]() 在x=1处的切线方程;
在x=1处的切线方程;
②求函数![]() 在
在![]() 上的最大,最小值.
上的最大,最小值.
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
【答案】(1)①![]() ;②函数
;②函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;(2)
;(2)![]() .
.
【解析】
(1)当![]() 时,求出函数
时,求出函数![]() 的导数.
的导数.
①根据导数的几何意义求出函数![]() 在x=1处的切线的斜率,写出切线的点斜式方程,最后化成一般形式即可;
在x=1处的切线的斜率,写出切线的点斜式方程,最后化成一般形式即可;
②根据导函数的正负性判断出函数的单调性,进而根据函数的极值定义求出函数的极值,再比较给定区间端点函数值进行求解即可;
(2)求出函数![]() 的导数,根据函数单调性和导数正负性的关系,得到不等式,常变量分离,构造新函数,判断新函数的单调性,求出新函数的最值进行求解即可.
的导数,根据函数单调性和导数正负性的关系,得到不等式,常变量分离,构造新函数,判断新函数的单调性,求出新函数的最值进行求解即可.
(1)当![]() 时,
时,![]() .
.
①当x=1时,![]() ,
,
所以函数![]() 在x=1处的切线的斜率为
在x=1处的切线的斜率为![]() ,因此切线方程为:
,因此切线方程为:
![]() ;
;
②因为![]() ,所以当
,所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,
,
而![]() ,
,
所以函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
(2)![]() ,
,
因为函数![]() 在
在![]() 上单调递增,
上单调递增,
所以 ![]() 在
在![]() 时恒成立,
时恒成立,
即![]() 在
在![]() 时恒成立,设
时恒成立,设![]() ,
,![]() ,
,
因为当![]() 时,函数
时,函数![]() 单调递增,所以
单调递增,所以![]() ,
,
因此要想![]() 在
在![]() 时恒成立,只需
时恒成立,只需![]() .
.
所以当函数![]() 在
在![]() 上单调递增时,实数
上单调递增时,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
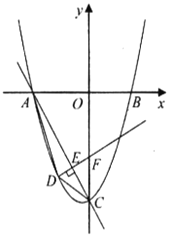
(1)求抛物线的解析式;
(2)如图,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,连结
下方抛物线上的一个动点,连结![]() .当
.当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)如图,在(2)的条件下,过点![]() 作于
作于![]() 点
点![]() 交
交![]() 轴于点
轴于点![]() 将
将![]() 绕点
绕点![]() 旋转得到
旋转得到![]() 在旋转过程中,当点
在旋转过程中,当点![]() 或点
或点![]() 落在
落在![]() 轴上(不与点
轴上(不与点![]()
![]() 重合)时,将
重合)时,将![]() 沿射线
沿射线![]() 平移得到
平移得到![]() ,在平移过程中,平面内是否存在点
,在平移过程中,平面内是否存在点![]() 使得四边形
使得四边形![]() 是菱形?若存在,请直接写出所有符合条件的点
是菱形?若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《复仇者联盟4:终局之战》是安东尼·罗素和乔·罗素执导的美国科幻电影,改编自美国漫威漫画,自2019年4月24日上映以来票房火爆.某电影院为了解在该影院观看《复仇者联盟4》的观众的年龄构成情况,随机抽取了100名观众的年龄,并分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,得到如图所示的频率分布直方图.
七组,得到如图所示的频率分布直方图.
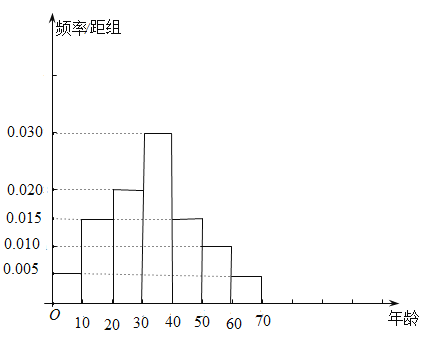
(1)求这100名观众年龄的平均数(同一组数据用该区间的中点值作代表)、中位数;
(2)该电影院拟采用抽奖活动来增加趣味性,观众可以选择是否参与抽奖活动(不参与抽奖活动按原价购票),活动方案如下:每张电影票价格提高10元,同时购买这样电影票的每位观众可获得3次抽奖机会,中奖1次则奖励现金![]() 元,中奖2次则奖励现金
元,中奖2次则奖励现金![]() 元,中奖三次则奖励现金
元,中奖三次则奖励现金![]() 元,其中
元,其中![]() 且
且![]() ,已知观众每次中奖的概率均为
,已知观众每次中奖的概率均为![]() .
.
①以某观众三次抽奖所获得的奖金总额的数学期望为评判依据,若要使抽奖方案对电影院有利,则![]() 最高可定为多少;
最高可定为多少;
②据某时段内的统计,当![]() 时该电影院有600名观众选择参加抽奖活动,并且
时该电影院有600名观众选择参加抽奖活动,并且![]() 每增加1元,则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变,抽奖活动给电影院带来的利润的期望为
每增加1元,则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变,抽奖活动给电影院带来的利润的期望为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.为检查该学校组织学生学习的效果,现从该校高一、高二、高三的学生中分别选取了4人,3人,3人作为代表进行问卷测试.具体要求:每位学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答.
(1)若从这10名学生中任选3人,求这3名学生分别来自三个年级的概率;
(2)若这10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记![]() 表示该名学生答对问题的个数,求随机变量
表示该名学生答对问题的个数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),设直线
为参数),设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并指出其曲线是什么曲线;
的参数方程化为普通方程,并指出其曲线是什么曲线;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 为曲线
为曲线![]() 上一动点,求
上一动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
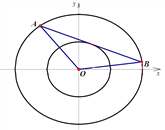
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种密码锁的密码设置是在正![]() 边形
边形![]() 的每个顶点处赋值0和1两个数中的一个,同时,在每个顶点处染红、蓝两种颜色之一,使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问:该种密码锁共有多少种不同的密码设置?
的每个顶点处赋值0和1两个数中的一个,同时,在每个顶点处染红、蓝两种颜色之一,使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问:该种密码锁共有多少种不同的密码设置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从境外回国的8位同胞中有1位被新冠肺炎病毒感染,需要通过核酸检测是否呈阳性来确定是否被感染.下面是两种检测方案:
方案一:逐个检测,直到能确定被感染者为止.
方案二:将8位同胞平均分为2组,将每组成员的核酸混合在一起后随机抽取一组进行检测,若检测呈阳性,则表明被感染者在这4位当中,然后逐个检测,直到确定被感染者为止;若检测呈阴性,则在另外一组中逐个进行检测,直到确定被感染者为止.
(1)根据方案一,求检测次数不多于两次的概率;
(2)若每次核酸检测费用都是100元,设方案二所需检测费用为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com