
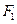 、
、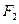 分别是椭圆C:
分别是椭圆C: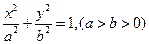 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 的弦AB两端点A、B与
的弦AB两端点A、B与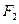 所成
所成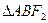 的周长是
的周长是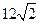 .
.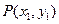 ,
,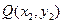 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段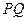 的中点为
的中点为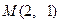 ,
,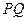 的方程
的方程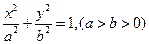 的焦距为2c,
的焦距为2c, 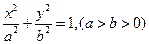 的焦距为2, ∴2c=6,即c=3…………1分
的焦距为2, ∴2c=6,即c=3…………1分 、
、 分别是椭圆C:
分别是椭圆C: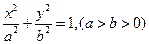 的左焦点和右焦点,且过
的左焦点和右焦点,且过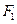 的弦AB两端点A、B与
的弦AB两端点A、B与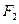 所成⊿AB
所成⊿AB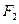 的周长是
的周长是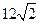 .
.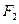 的周长 = AB+(AF2+BF2)= (AF1+BF1)+ (AF2+BF2)=4
的周长 = AB+(AF2+BF2)= (AF1+BF1)+ (AF2+BF2)=4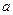 =
=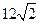
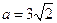 …………4分
…………4分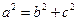 , ∴
, ∴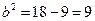 ∴椭圆C的方程是
∴椭圆C的方程是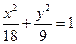 …………6分
…………6分 点
点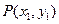 ,
,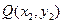 是椭圆C上不同的两点,
是椭圆C上不同的两点,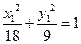 ,
,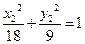 .…………7分
.…………7分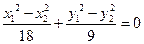 ,…………8分
,…………8分 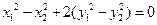 ,
,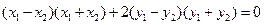 ,…9分
,…9分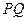 的中点为
的中点为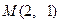 ,∴
,∴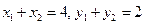 . …10分
. …10分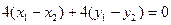 ,…………11分
,…………11分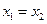 ,由上式知,
,由上式知,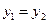 则
则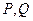 重合,与已知矛盾,因此
重合,与已知矛盾,因此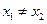 ,………12分
,………12分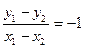 . ……………………13分
. ……………………13分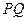 的方程为
的方程为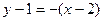 ,即
,即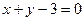 . ………14分
. ………14分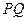 的不存在时,
的不存在时, 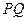 的中点在
的中点在 轴上, 不符合题意.
轴上, 不符合题意.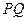 的方程为
的方程为 ,
,  . ……8分
. ……8分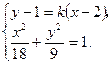 消去
消去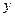 ,得
,得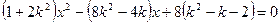 (*)
(*) . ………10分
. ………10分
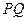 的中点为
的中点为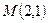 ,
,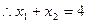 .
.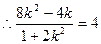 .解得
.解得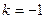 . ………12分
. ………12分  ,其判别式
,其判别式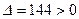 .………13分
.………13分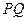 的方程为
的方程为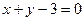 . ………14分
. ………14分 

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:不详 题型:解答题
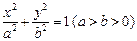 的左、右焦点,点P(-1,
的左、右焦点,点P(-1,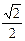 )在椭圆上,线段PF2与
)在椭圆上,线段PF2与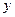 轴的交点
轴的交点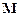 满足
满足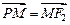 .(1)求椭圆的标准方程;
.(1)求椭圆的标准方程;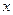 轴重合的直线
轴重合的直线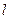 ,
,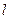 与圆
与圆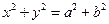 相交于A、B.并与椭圆相交于C、D.当
相交于A、B.并与椭圆相交于C、D.当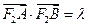 ,且
,且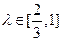 时,求△F2CD的面积S的取值范围.
时,求△F2CD的面积S的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
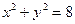 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线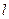 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线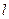 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.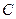 的方程;
的方程; 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 PMN的面积为
PMN的面积为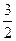 ,点A的坐标为(1+
,点A的坐标为(1+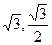 ),
), 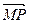 =m·
=m·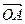 (m为常数),
(m为常数),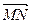
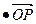
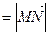
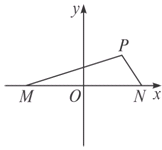
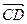 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
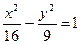 与椭圆
与椭圆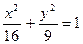 有共同的准线;
有共同的准线;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com