
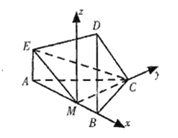
【题目】如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,CM⊥AB,垂足为M,且AE=AC=2![]() ,BD=2BC=4,
,BD=2BC=4,
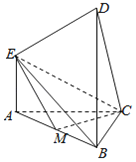
(1)求证:CM⊥ME;
(2)求二面角A﹣MC﹣E的余弦值.
(3)在线段DC上是否存在一点N,使得直线BN∥平面EMC,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析(2)![]() ;(3)存在,
;(3)存在,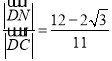 .
.
【解析】
(1)根据已知可得AE⊥CM,进而证明CM⊥平面EAM,即可证明结论;
(2)由(1)得出二面角A﹣MC﹣E的平面角为∠AME,解直角三角形AME,即可求出结论;
(3)以M为原点,建立空间直角坐标系,设![]() ,求出
,求出![]() 坐标和平面
坐标和平面![]() 法向量坐标,即可求解.
法向量坐标,即可求解.
(1)∵EA⊥平面ABC;∴AE⊥CM,
又∵CM⊥AB且AB,EM相交于M点,且在平面EAM内;
∴CM⊥平面EAM,∴CM⊥ME.
(2)由(1)知道,∠AME为所求的平面角;
![]() ,
,
![]()
∴![]() ;
;
![]() ,
,
![]() ,
,
所以所求二面角的余弦值为![]() ;
;
(3)以M为原点,分别以MB,MC,为x,y轴,建立空间直角坐标系;
在△ABC,可得MB=1,MA=3,MC![]() ;
;
则![]() ,B(1,0,0),D(1,0,4),
,B(1,0,0),D(1,0,4),![]()
![]() ,
,![]()
设平面EMC的一个法向量![]() ;
;
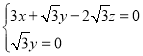 ,取x=2,得
,取x=2,得![]()
设![]() ;∴
;∴![]() ;
;
∵BN∥平面EMN;
∴![]() ;
;
所以![]() ;
;
故线段DC上存在一点N,使得直线BN∥平面EMC,
且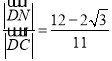 .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=![]() ,AP=
,AP=![]() ,PC=
,PC=![]() .
.
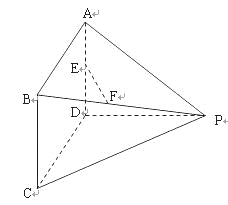
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
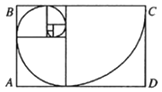
【题目】若数列{an}满足a1=1,a2=1,an+2=an+an+1,则称数列{an}为斐波那契数列,斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例.作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个圆心角为90°的扇形,连起来的弧线就是斐波那契螺旋线,如图所示的7个正方形的边长分别为a1,a2,…,a7,在长方形ABCD内任取一点,则该点不在任何一个扇形内的概率为( )
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能,近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 6.1 | 7.1 | 9.7 | 12.2 |
某位同学分别用两种模型:①![]() ,②
,②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
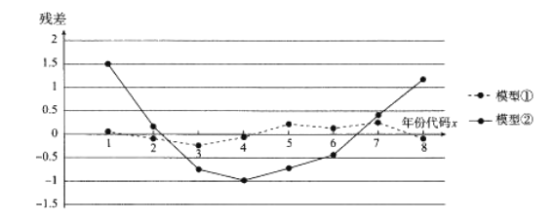
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() )
)
经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立![]() 关于
关于![]() 的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:归直线的斜率和截距的最小二乘估计公式分别为: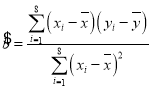 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:![]() 1(a>b>0)的长轴长为2
1(a>b>0)的长轴长为2![]() ,离心率为
,离心率为![]() ,过点(0,1)的直线l与M交于A,B两点,且
,过点(0,1)的直线l与M交于A,B两点,且![]() .
.
(1)求M的方程;
(2)求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点,![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() ,
,![]() 的点,若
的点,若![]() 的边长为4的等边三角形.
的边长为4的等边三角形.
![]() 写出椭圆的标准方程;
写出椭圆的标准方程;
![]() 当直线
当直线![]() 的一个方向向量是
的一个方向向量是![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
![]() 设点R满足:
设点R满足:![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 1(a>b>0)的焦距F1F2的长为2,经过第二象限内一点P(m,n)的直线
1(a>b>0)的焦距F1F2的长为2,经过第二象限内一点P(m,n)的直线![]() 1与圆x2+y2=a2交于A,B两点,且OA
1与圆x2+y2=a2交于A,B两点,且OA![]() .
.
(1)求PF1+PF2的值;
(2)若![]()
![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家“十三五”计划,提出创新兴国,实现中国创新,某市教育局为了提高学生的创新能力,把行动落到实处,举办一次物理、化学综合创新技能大赛,某校对其甲、乙、丙、丁四位学生的物理成绩(x)和化学成绩(y)进行回归分析,求得回归直线方程为![]() =1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
=1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
甲 | 乙 | 丙 | 丁 | |
物理成绩(x) | 75 | m | 80 | 85 |
化学成绩(y) | 80 | n | 85 | 95 |
综合素质 (x+y) | 155 | 160 | 165 | 180 |
(1)请设法还原乙的物理成绩m和化学成绩n;
(2)在全市物理化学科技创新比赛中,由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛,每场比赛均由赛事主办方从学校代表中随机抽两人参赛,每场比赛所抽的选手中,只要有一名选手的综合素质分高于160分,就能为所在学校赢得一枚荣誉奖章.若记比赛中赢得荣誉奖章的枚数为ξ,试根据上表所提供数据,预测该校所获奖章数ξ的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com