
【题目】![]() 的展开式中,
的展开式中,![]() 的系数是( )
的系数是( )
A. -160 B. -120 C. 40 D. 200
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将参加夏令营的400名学生编号为:001,002,…,400,采用系统抽样的方法抽取一个容量为40的样本,且随机抽得的号码为003,这400名学生分住在三个营区,从001到180在第一营区,从181到295在第二营区,从296到400在第三营区,三个营区被抽中的人数分别为( )
A. 18,12,10 B. 20,12,8 C. 17,13,10 D. 18,11,11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
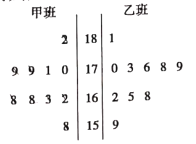
(1)计算甲班的样本方差;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为
的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(1)求椭圆C的标准方程:
(2)设点P为椭圆C的下顶点,直线PA,PB与y=2分别交于点M,N,当|MN|最小时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N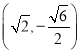 .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com