
(本小题满分12分)
某工厂修建一个长方体无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的 造价为150元,池壁每平方米的造价为120元.设池底长方形长为 米.
米.
(1)求底面积,并用含 的表达式表示池壁面积;
的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
(1)池壁面积为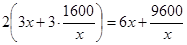 (平方米);
(平方米);
(2)池底设计为边长40米的正方形时总造价最低,为297600元。
解析试题分析:(Ⅰ)分析题意,本小题是一个建立函数模型的问题,可设水池的底面积为S1,池壁面积为S2,由题中所给的关系,将此两者用池底长方形长x表示出来.
(Ⅱ)此小题是一个花费最小的问题,依题意,建立起总造价的函数解析式,由解析式的结构发现,此函数的最小值可用基本不等式求最值,从而由等号成立的条件求出池底边长度,得出最佳设计方案
解:(1)由题意水池底面积为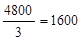 (平方米) 3分
(平方米) 3分
池壁面积为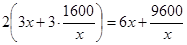 (平方米) 6分
(平方米) 6分
(2)设水池总造价为 元,则
元,则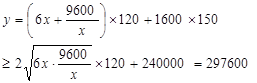 10分
10分
当且仅当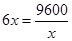 即
即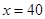 时取等号。
时取等号。
故池底设计为边长40米的正方形时总造价最低,为297600元。 12分
考点:本题主要考查函数模型的选择与应用。
点评:解题的关键是建立起符合条件的函数模型,故分析清楚问题的逻辑联系是解决问题的重点,此类问题的求解的一般步骤是:建立函数模型,进行函数计算,得出结果,再将结果反馈到实际问题中指导解决问题


科目:高中数学 来源: 题型:解答题
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为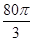 立方米,且
立方米,且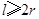 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为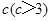 千元,设该容器的建造费用为
千元,设该容器的建造费用为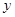 千元.
千元.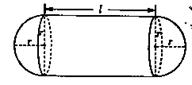
(Ⅰ)写出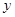 关于
关于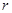 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的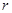 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)已知f(x)=m(x-2m)(x+m+3),g(x)=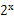 -2,若同时满足条件:
-2,若同时满足条件:
①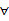 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②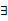 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com