
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(1) 7.(2) 0.4
解析试题分析:解 (1)∵这6位同学的平均成绩为75分,
∴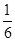 (70+76+72+70+72+x6)=75,
(70+76+72+70+72+x6)=75,
解得x6=90, 3分
这6位同学成绩的方差
s2=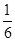 ×[(70-75)2+(76-75)2+(72-75)2+(70-75)2+(72-75)2+(90-75)2]=49,
×[(70-75)2+(76-75)2+(72-75)2+(70-75)2+(72-75)2+(90-75)2]=49,
∴标准差s=7 6分
(2)从前5位同学中,随机地选出2位同学的成绩有:(70,76),(70,72),(70,70),(70,72),(76,72),(76,70),(76,72),(72,70),(72,72),(70,72),共10种, 9分
恰有1位同学成绩在区间(68,75)中的有:(70,76),(76,72),(76,70),(76,72),共4种,所求的概率为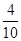 =0.4 11分
=0.4 11分
即恰有1位同学成绩在区间(68,75)中的概率为0.4 12分
考点:方差,古典概型
点评:解决的关键是根据方差的定义得到求解,以及古典概型 概率公式来得到概率值,属于基础题。


科目:高中数学 来源: 题型:解答题
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.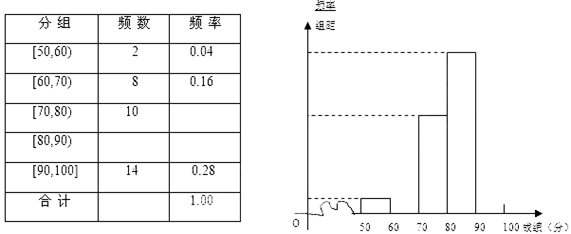
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
广告费支出 | 2 | 4 | 5 | 6 | 8 |
销售额 | 30 | 40 | 60 | 50 | 70 |
 ,
,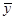 的值并求点
的值并求点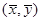 对应的复数
对应的复数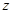 ;
; 。
。 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
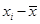 | | | | | |
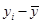 | | | | | |
 | | | | | |
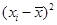 | | | | | |
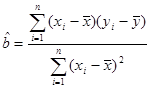 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示。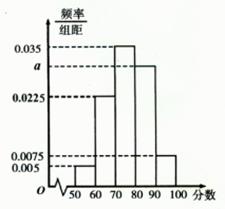
(1)请根据图中所给数据,求出 的值;
的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[ 60,70)内的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)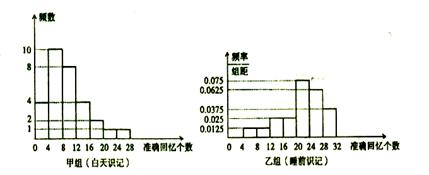
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后
驾车和醉酒驾车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布
直方图.
(1)根据频率分布直方图,求此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为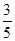 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: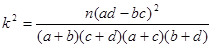
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
 | 文艺节目 | 新闻节目 | 总计 |
| 20~40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布条形图,解答下列问题:
(1)求频率分布表中的 ,
,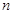 值,并补全频数条形图;
值,并补全频数条形图;
(2)根据频数条形图估计该样本的中位数是多少?
(3)若成绩在65.5~85.5分的学生为三等奖,问该校获得三等奖的学生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com