
【题目】设函数f(x)=lnx,g(x)=(2﹣a)(x﹣1)﹣2f(x). (Ⅰ)当a=1时,求函数g(x)的单调区间;
(Ⅱ)设F(x)=|f(x)|+ ![]() (b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有
(b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有 ![]() <﹣1,求实数b的取值范围.
<﹣1,求实数b的取值范围.
【答案】解:(Ⅰ)当a=1时,g(x)=x﹣1﹣2lnx,(x>0), ∴g′(x)=1﹣ ![]() =
= ![]() ,
,
当x∈(0,2)时,g′(x)<0,g(x)单调递减,
当x∈(2,+∞)时,g′(x)>0,g(x)单调递增,
综上,g(x)的递减区间是(0,2),递增区间是(2,+∞);
(Ⅱ)由题意得: ![]() +1<0,即
+1<0,即 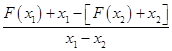 <0,
<0,
若设G(x)=F(x)+x,则G(x)在(0,2]上单调递减,
① 当x∈[1,2]时,G(x)=lnx+ ![]() +x,G′(x)=
+x,G′(x)= ![]() ﹣
﹣ ![]() +1≤0,
+1≤0,
b≥ ![]() +(x+1)2=x2+3x+3+
+(x+1)2=x2+3x+3+ ![]() ,
,
设G1(x)=x2+3x+3+ ![]() ,则G1′(x)=2x+3﹣
,则G1′(x)=2x+3﹣ ![]() >0在(1,2)恒成立,
>0在(1,2)恒成立,
∴G1(x)在(1,2]单调递增,
∴b≥G1(x)max=G2(2)= ![]() ;
;
②当x∈(0,1)时,G(x)=﹣lnx+ ![]() +x,G′(x)=x2+x﹣
+x,G′(x)=x2+x﹣ ![]() ﹣1,
﹣1,
设G2(x)=x2+x﹣ ![]() ﹣1,则G2′(x)=2x+1+
﹣1,则G2′(x)=2x+1+ ![]() >0,
>0,
即G2′(x)=2x+1+ ![]() >0,即G2(x)在(0,1)单调递增,
>0,即G2(x)在(0,1)单调递增,
故G2(x)≤G2(1)=0,
∴b≥0,
综上,由①②可得:b≥ ![]()
【解析】(Ⅰ)将a=1代入g(x)的表达式,求出g(x)的导数,从而求出函数的单调区间;(Ⅱ)问题转化为 ![]() <0,若设G(x)=F(x)+x,通过讨论①当x∈[1,2]时,②当x∈(0,1)时,G(x)的单调性,从而得到b的范围.
<0,若设G(x)=F(x)+x,通过讨论①当x∈[1,2]时,②当x∈(0,1)时,G(x)的单调性,从而得到b的范围.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】三国时期吴国的数学家赵爽创制了一幅“勾股方圆图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股方圆图”中,四个全等的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角![]() ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内![]() 含20小时
含20小时![]() 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
![]() 设在A俱乐部租一块场地开展活动x小时的收费为
设在A俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,在B俱乐部租一块场地开展活动x小时的收费为
,在B俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,试求
,试求![]() 与
与![]() 的解析式;
的解析式;
![]() 问该企业选择哪家俱乐部比较合算,为什么?
问该企业选择哪家俱乐部比较合算,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
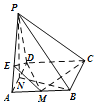
【题目】如图,四棱锥![]() 的底面ABCD是正方形,
的底面ABCD是正方形,![]() 为等边三角形,M,N分别是AB,AD的中点,且平面
为等边三角形,M,N分别是AB,AD的中点,且平面![]() 平面ABCD.
平面ABCD.
![]() 证明:
证明:![]() 平面PNB;
平面PNB;
![]() 设点E是棱PA上一点,若
设点E是棱PA上一点,若![]() 平面DEM,求
平面DEM,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-7x+6<0},B={x|4-t<x<t},R为实数集.
(1)当t=4时,求A∪B及A∩RB;
(2)若A∪B=A,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点. 
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2 ![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.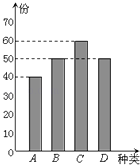
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x个月的利润  (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率 ![]() ,例如:
,例如: ![]() .
.
(1)求g(10);
(2)求第x个月的当月利润率g(x);
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com