
【题目】在平面直角坐标系xOy中,已知双曲线![]() .
.
(1)过![]() 的左顶点引
的左顶点引![]() 的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交![]() 于P,Q两点,若l与圆
于P,Q两点,若l与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() ,若M,N分别是
,若M,N分别是![]() ,
,![]() 上的动点,且
上的动点,且![]() ,求证:O到直线MN的距离是定值.
,求证:O到直线MN的距离是定值.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据题意,写出双曲线的左顶点,求出直线的方程,联立求得三角形顶点坐标,之后利用三角形的面积公式求得结果.
(2)设直线![]() 的方程为
的方程为![]() ,通过直线
,通过直线![]() 与已知圆相切,得到
与已知圆相切,得到![]() ,通过求解
,通过求解![]() .证明
.证明![]() .
.
(3)当直线![]() 垂直
垂直![]() 轴时,直接求出
轴时,直接求出![]() 到直线
到直线![]() 的距离为
的距离为![]() .当直线
.当直线![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为:
的方程为:![]() ,(显然
,(显然![]() ),推出直线
),推出直线![]() 的方程为
的方程为![]() ,求出
,求出![]() ,
,![]() ,设
,设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,通过
,通过![]() ,求出
,求出![]() .推出
.推出![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
(1)根据题意可得![]() 的左顶点为
的左顶点为![]() ,
,
设直线方程为![]() ,
,
与另一条渐近线![]() 联立求得交点坐标为
联立求得交点坐标为![]() ,
,
所以对应三角形的面积为![]() ;
;
(2)设直线![]() 的方程是
的方程是![]() ,因直线与已知圆相切,
,因直线与已知圆相切,
故![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,
故![]() ;
;
(3)当直线ON垂直于x轴时,![]() ,
,![]() ,
,![]()
则O到直线MN的距离为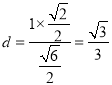 .
.
当直线![]() 不垂直于
不垂直于![]() 轴时,
轴时,
设直线![]() 的方程为
的方程为![]() (显然
(显然![]() ),
),
则直线![]() 的方程为
的方程为![]() .
.
由![]() 与椭圆方程联立,
与椭圆方程联立,
得![]() ,
,![]() ,所以
,所以![]() .
.
同理![]() .
.
设O到直线MN的距离为d,
则由![]() ,
,
得 .
.
综上,O到直线MN的距离是定值![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标平面![]() 上的一列点
上的一列点![]() ,简记为
,简记为![]() .若由
.若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,其中
,其中![]() 为方向与
为方向与![]() 轴正方向相同的单位向量,则称
轴正方向相同的单位向量,则称![]() 为
为![]() 点列.
点列.
(1)判断![]() ,是否为
,是否为![]() 点列,并说明理由;
点列,并说明理由;
(2)若![]() 为
为![]() 点列,且点
点列,且点![]() 在点
在点![]() 的右上方.任取其中连续三点
的右上方.任取其中连续三点![]() ,判断
,判断![]() 的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若![]() 为
为![]() 点列,正整数
点列,正整数![]() ,满足
,满足![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年2月份,我国武汉地区爆发了新冠肺炎疫情,为了预防疫情蔓延,全国各大医药厂商纷纷加紧生产口罩,某医疗器械生产工厂为了解目前的生产力,统计了每个工人每小时生产的口罩数量(单位:箱),得到如图所示的频率分布直方图,其中每个工人每小时的产量均落在[10,70]内,数据分组为[10,20)、[20,30)、[30,40)、[40,50)、[50,60)、![]() ,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为
,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为![]() .
.
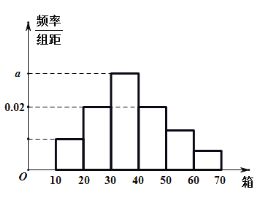
(1)求实数a的值;
(2)在最后三组中采用分层抽样的方法随机抽取了6人,现从这6人中随机抽出两人对其它小组的工人进行生产指导,求这两人来自同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是椭圆W:![]() 上的三个点,O是坐标原点.
上的三个点,O是坐标原点.
(I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积.
(II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某疫苗进行安全性临床试验.该疫苗安全性的一个重要指标是:注射疫苗后人体血液中的高铁血红蛋白(MetHb)的含量(以下简称为“M含量”)不超过1%,则为阴性,认为受试者没有出现高铁血红蛋白血症(简称血症);若M含量超过1%,则为阳性,认为受试者出现血症.若一批受试者的M含量平均数不超过0.65%,且出现血症的被测试者的比例不超过5%,则认为该疫苗在M含量指标上是“安全的”;否则为“不安全”.现有男、女志愿者各200名接受了该疫苗注射,按照性别分层,随机抽取50名志愿者进行M含量的检测,其中女性志愿者被检测出阳性的恰好1人.经数据整理,制得频率分布直方图如下.(注:在频率分布直方图中,同一组数据用该区间的中点值作代表.)
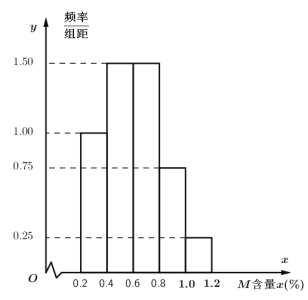
(1)请说明该疫苗在M含量指标上的安全性;
(2)请利用样本估计总体的思想,完成这400名志愿者的![]() 列联表,并判断是否有超过99%的把握认为,注射疫苗后,高铁血红蛋白血症与性别有关?
列联表,并判断是否有超过99%的把握认为,注射疫苗后,高铁血红蛋白血症与性别有关?
男 | 女 | |
阳性 | ||
阴性 |
附: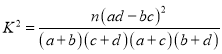 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com