已知动点P(x,y)到点F(0,1)与到直线y=-1的距离相等,
(1)求点P的轨迹L的方程;
(2) 若正方形ABCD的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)(x1<0≤x2<x3)在(1)中的曲线L上,设BC的斜率为k,l=|BC|,求l关于k的函数解析式l=f(k);
(3)求(2)中正方形ABCD面积S的最小值.
【答案】
分析:(1)利用抛物线的定义得到点P的轨迹是抛物线;利用抛物线的方程写出轨迹方程.
(2)利用直线方程的点斜式设出直线AB,BC,将两直线方程分别于抛物线联立;利用韦达定理及弦长公式表示出AB,BC;由正方形的边长相等,得到斜率与坐标的关系,代入BC中,得到函数解析式l=f(k).
(3)求面积的最小值即求BC的最小值,利用基本不等式求出正方形边长的最小值.
解答:解:(1)由题设可得动点P的轨迹方程为x
2=4y.(4分)
(2)由(1),可设直线BC的方程为:
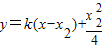
(k>0),

,
易知x
2、x
3为该方程的两个根,故有x
2+x
3=4k,得x
3=4k-x
2,
从而得
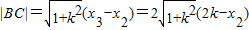
(6分)
类似地,可设直线AB的方程为:
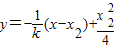
,
从而得
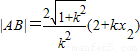
,(8分)
由|AB|=|BC|,得k
2•(2k-x
2)=(2+kx
2),
解得
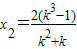
,

(k>0).(10分)
(3)因为
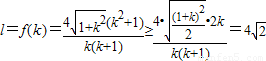
,(12分)
所以S=l
2≥32,即S的最小值为32,
当且仅当k=1时取得最小值.(14分)
点评:本题考查求曲线轨迹方程的常用方法:定义法;考查直线与圆锥曲线的位置关系常用的处理方法是将方程联立用韦达定理,考查直线与圆锥曲线相交得到的弦长公式;利用基本不等式求函数最值需满足:一正、二定、三相等.

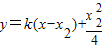 (k>0),
(k>0), ,
,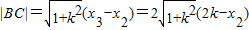 (6分)
(6分)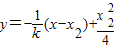 ,
,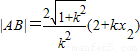 ,(8分)
,(8分)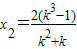 ,
, (k>0).(10分)
(k>0).(10分)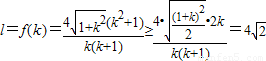 ,(12分)
,(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案