
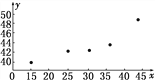
����Ŀ���ٶ�С���������x���������Ч��y֮�������ع�ϵ������5���������£�
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)��xΪ���ͱ�����yΪԤ������������ɢ��ͼ��
(2)��y��x֮������Իع鷽�̣����ڻ�������56.7Ԥ������Ч�룻
(3)�������в������в�ƽ���ͣ�
(4)��R2����˵���в��������Ч���Ӱ��ռ�ٷ�֮����
���𰸡�(1)������ ��2��![]() ��0.29x��34.708�����Ƴ�������Ч��51.151. (3)
��0.29x��34.708�����Ƴ�������Ч��51.151. (3) ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.
��1.616. ![]() ��8.521 30.(4) R2��0.830���в����������Լ1��83%��17%.
��8.521 30.(4) R2��0.830���в����������Լ1��83%��17%.
�����������������(1)��������ϵ���ݸ���ֵ���ÿ���㼴�ɣ�2����ͼ���������������״�ֲ����бȽϺõ�������ع�ϵ����˿��������Իع鷽�̻̿�����֮��Ĺ�ϵ�����ݱ������ݣ�����![]() ��
�� ![]() ��
��![]() д�����Իع鷽�̣�����x��56.7ʱ���ý⣨3������y��bx��a��e���������
д�����Իع鷽�̣�����x��56.7ʱ���ý⣨3������y��bx��a��e���������![]() ��yi��
��yi��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.������ͼ����ܲв�ƽ���ͣ�4��������ƫ��ƽ���ͣ��ع�ƽ����=��ƫ��ƽ����-�в�ƽ���ͣ����빫ʽ��R2�����ͱ���С�������������ЧӦ�����ã��в����������.
��1.616.������ͼ����ܲв�ƽ���ͣ�4��������ƫ��ƽ���ͣ��ع�ƽ����=��ƫ��ƽ����-�в�ƽ���ͣ����빫ʽ��R2�����ͱ���С�������������ЧӦ�����ã��в����������.
���������
(1)����ͼ��ʾ��
(2)��ͼ���������������״�ֲ����бȽϺõ�������ع�ϵ����˿��������Իع鷽�̻̿�����֮��Ĺ�ϵ����ع鷽��Ϊ![]() ��
��![]() x��
x��![]() ��
��![]() ��30.316��
��30.316��![]() ��43.5��
��43.5��![]() ��5 090.256 4��
��5 090.256 4��
![]() ��
��![]() ��1 318.746��
��1 318.746��![]() 2��1 892.25��
2��1 892.25��![]() 2��919.059 9��
2��919.059 9��
![]() iyi��6 737.322.
iyi��6 737.322.
��![]() ��
��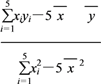 ��0.29.
��0.29.![]() ��
��![]() ��
��![]()
![]() ��34.708.
��34.708.
����������Իع鷽��Ϊ![]() ��0.29x��34.708.
��0.29x��34.708.
��x��56.7ʱ��![]() ��0.29��56.7��34.708��51.151�����Ƴ�������Ч��51.151.
��0.29��56.7��34.708��51.151�����Ƴ�������Ч��51.151.
(3)����y��bx��a��e���������![]() i��yi��
i��yi��![]() i�ֱ�Ϊ
i�ֱ�Ϊ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.
��1.616.
�в�ƽ���ͣ�![]() ��8.521 30.
��8.521 30.
(4)��ƫ��ƽ���ͣ�![]() (yi��
(yi��![]() )2��50.18��
)2��50.18��
�ع�ƽ���ͣ�50.18��8.521 30��41.658 7��
R2��0.830.
����ͱ���С�������������ЧӦ������Լ83%.
�в����������Լ1��83%��17%.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() �ڵ�
�ڵ�![]() ��������б��Ϊ1������
��������б��Ϊ1������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��2���躯��![]() ��
��![]() .������
.������![]() ����Сֵ��
����Сֵ��![]() ����
����![]() ��ֵ��
��ֵ��
��3��������![]() ��
��![]() �Ķ�������
�Ķ�������![]() �����ں���
�����ں���![]() ��ͼ���ϵ�����һ��
��ͼ���ϵ�����һ��![]() ���ں���
���ں���![]() ��ͼ���϶�����һ��
��ͼ���϶�����һ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ����Ȼ�����ĵ�����
����Ȼ�����ĵ�����![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ�У���![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
Ϊ������ ![]() ����ֱ��
����ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ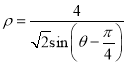 .
.
��1��д������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��![]() ����
Ϊ����![]() ������һ�㣬
������һ�㣬 ![]() Ϊֱ��
Ϊֱ��![]() ����һ�㣬��
����һ�㣬��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߿Ƽ���ҵ������ƷA�Ͳ�ƷB��Ҫ�ס����������Ͳ��ϣ�����һ����ƷA��Ҫ�ײ���1.5 kg���Ҳ���1 kg����5����ʱ������һ����ƷB��Ҫ�ײ���0.5 kg���Ҳ���0.3 kg����3����ʱ������һ����ƷA������Ϊ2 100Ԫ������һ����ƷB������Ϊ900Ԫ������ҵ���мײ���150 kg���Ҳ���90 kg�����ڲ�����600����ʱ�������£�������ƷA����ƷB������֮�͵����ֵΪ________________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ�μ���ѧ�Ļ�֪ʶ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴβ��Գɼ��������ȡ8�Σ���¼���£�

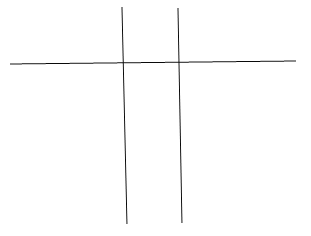
�����þ�Ҷͼ��ʾ���������ݣ�
������Ҫ����ѡ��һ�˲μ���ʽ������������ȡ��������������ס�����λͬѧ��ƽ��ֵ�ͷ���ݴ�����Ϊѡ����λͬѧ�μӱ�����Ϊ���ʣ�
�������Լ�ͬѧ����ʽ�����ɼ�����Ԥ�⣬������ɼ�����80�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�� ![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬
��һ�㣬 ![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
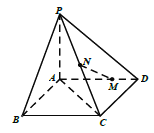
��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д����������ķ����ж�����٣�
(1)p��ĩλ����Ϊ9�������ܱ�3������
(2)p���е�������ż����
(3)p��������һ��ʵ��x��ʹx2��1��0��
(4)p��x��y��R��x2��y2��2x��4y��5��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ��ΪC��Բ����x��a��2+��y��b��2=8��a��bΪ������������A��0��1��������ֱ��y��3��2 ![]() =0���У�
=0����
��1����ԲC�ķ��̣�
��2��������M��4����1����ֱ��l��ԲC�ཻ��E��F���㣬�� ![]() =0����ֱ��l�ķ��̣�
=0����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com