
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A作直线m,与圆O相交于两点R,S,若△ORS是钝角三角形,求直线m的斜率k的取值范围.
【答案】
(1)
解:由题意可得e= ![]() =
= ![]() ,
,
又圆O的方程为x2+y2=b2,
因为直线l:x﹣y+2=0与圆O相切,
b= ![]() ,由a2=3c2=3(a2﹣b2),即a2=3.
,由a2=3c2=3(a2﹣b2),即a2=3.
所以椭圆C的方程为 ![]()
(2)
解:由(1)得知圆的方程为x2+y2=2.A(﹣ ![]() ,0),直线m 的方程为:y=k(x+
,0),直线m 的方程为:y=k(x+ ![]() ).
).
设R(x1,y1),S(x2,y2),由 ![]()
得 ![]()
![]() ,
,
由△=12k4﹣4(1+k2)(3k2﹣2)>0的﹣ ![]() <k<
<k< ![]() …①
…①
因为△ORS是钝角三角形,∴ ![]() =
= ![]() =
= ![]() .
.
![]() …②
…②
由A、R、S三点不共线,知k≠0. ③
由①、②、③,得直线m的斜率k的取值范围是(﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
【解析】(1)求得圆O的方程,运用直线和相切的条件:d=r,求得b,再由离心率公式和a,b,c的关系,可得a,进而得到椭圆方程;(2)先设出点R,S的坐标,利用△ORS是钝角三角形,求得 ![]() =x1x2+y1y2<0,从而求出斜率k的取值范围
=x1x2+y1y2<0,从而求出斜率k的取值范围


科目:高中数学 来源: 题型:
【题目】已知t为实数,函数![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(2)当![]() 时,
时,![]() 的图象始终在
的图象始终在![]() 的图象的下方,求t的取值范围;
的图象的下方,求t的取值范围;
(3)设![]() ,当
,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数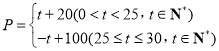 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机在数据处理时使用的是二进制,例如十进制的1、2、3、4在二进制分别表示为1、10、11、100.下面是某同学设计的将二进制数11111化为十进制数的一个流程图,则判断框内应填入的条件是( ) 
A.i>4
B.i≤4
C.i>5
D.i≤5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的长轴长
的长轴长![]() ,短轴长
,短轴长![]() .
.

(1)求椭圆的方程;
(2)记椭圆的左右顶点![]() ,分别过
,分别过![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,
,![]() 为 椭圆上位于
为 椭圆上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
(i)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 的面积;
的面积;
(ii)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com