a,b是正实数,且a+b=4,则

有
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知
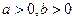
,求证:
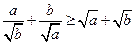
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知各项均为正数的数列

满足

其中
n=1,2,3,….(1)求

的值;(2)求证:

;

查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设变量x、y满足约束条件

的最大值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
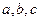
为正数,且
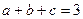
,则
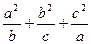
的最小值是__________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设不等式组
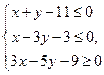
表示的区域为D,若对数函数
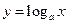
的图象上存在区域D上的点,则a的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若不等式组

表示的平面区域是一个三角形,则
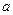
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
(不等式选讲选做题)
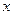
、
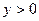
,
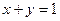
,则
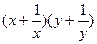
的最小值为______.
查看答案和解析>>

 名校课堂系列答案
名校课堂系列答案