
【题目】已知数列![]() 前
前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)证明数列![]() 是等比数列;
是等比数列;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)数列![]() 是以
是以![]() 为首项,以2为公比的等比数列. (2)
为首项,以2为公比的等比数列. (2) ![]()
【解析】试题分析:(1)当![]() 时,
时, ![]() ,可得以
,可得以![]() ,所以数列
,所以数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列;(2)由(1)知,
为公比的等比数列;(2)由(1)知, ![]() ,可得
,可得![]() ,利用错位相减法可得数列
,利用错位相减法可得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() ,
,
所以数列![]() 是以
是以![]() 为首项,以2为公比的等比数列.
为首项,以2为公比的等比数列.
(2)由(1)知, ![]() ,
,
所以![]() ,
,
所以![]() (1)
(1)
![]() (2)
(2)
(1)-(2)得:
![]()
![]()
![]() ,
,
所以![]() .
.
【 方法点睛】本题主要考查等比数列的通项公式与求和公式以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内画1条线段,将圆分割成两部分;画2条相交线段,彼此分割成4条线段,将圆分割成4部分;画3条线段,彼此最多分割成9条线段,将圆最多分割成7部分;画4条线段,彼此最多分割成16条线段,将圆最多分割成11部分.那么




(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分割成多少部分?
(2)猜想:圆内两两相交的n条线段,彼此最多分割成多少条线段?
(3)猜想:在圆内画n条线段,两两相交,将圆最多分割成多少部分?
并用数学归纳法证明你所得到的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
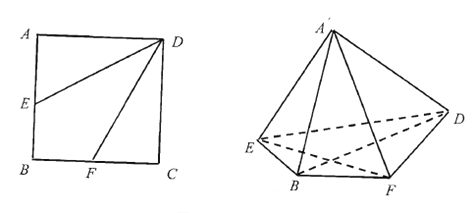
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com