【题目】将函数
的图象向左平移
个单位长度，再向上平移1个单位长度，得到函数g（x）的图象，则函数g（x）具有性质_____．（填入所有正确结论的序号）
①最大值为
，图象关于直线
对称；
②图象关于y轴对称；
③最小正周期为π；
④图象关于点
对称．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，方程f2（x）﹣af（x）+b=0（b≠0）有六个不同的实数解，则3a+b的取值范围是（ ）
A.[6，11]
B.[3，11]
C.（6，11）
D.（3，11）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，棱长为1（单位：
）的正方体木块经过适当切割，得到几何体
，已知几何体由两个底面相同的正四棱锥组成，底面
平行于正方体的下底面，且各顶点均在正方体的面上，则几何体体积的取值范围是________（单位：
）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于序列A0：a0 ， a1 ， a2 ， …，an（n∈N*），实施变换T得序列A1：a1+a2 ， a2+a3 ， …，an﹣1+an ， 记作A1=T（A0）：对A1继续实施变换T得序列A2=T（A1）=T（T（A0）），记作A2=T2（A0）；…；An﹣1=Tn﹣1（A0）．最后得到的序列An﹣1只有一个数，记作S（A0）． （Ⅰ）若序列A0为1，2，3，求S（A0）；
（Ⅱ）若序列A0为1，2，…，n，求S（A0）；
（Ⅲ）若序列A和B完全一样，则称序列A与B相等，记作A=B，若序列B为序列A0：1，2，…，n的一个排列，请问：B=A0是S（B）=S（A0）的什么条件？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角梯形ABCD中，AD∥BC, AB⊥BC, BD⊥DC，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE, AC, DE,得到如图所示的空间几何体．
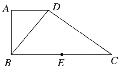
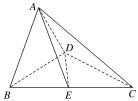
(1)求证：AB⊥平面ADC；
(2)若AD＝1，AB＝
，求点B到平面ADE的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=|x+2|+|x﹣a|，x∈R
（1）若a＜0，且log2f（x）＞2对任意x∈R恒成立，求实数a的取值范围；
（2）若a＞0，且关于x的不等式f（x）＜ 
x有解，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，椭圆
：
的离心率为
，焦点到相应准线的距离为
，
，
分别为椭圆的左顶点和下顶点，
为椭圆上位于第一象限内的一点，
交
轴于点
，
交
轴于点
.
（1）求椭圆的标准方程；
（2）若
，求
的值；
（3）求证：四边形
的面积为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知M（ 
，0），N（2，0），曲线C上的任意一点P满足： 
= 
| 
|．
（Ⅰ）求曲线C的方程；
（Ⅱ）设曲线C与x轴的交点分别为A、B，过N的任意直线（直线与x轴不重合）与曲线C交于R、Q两点，直线AR与BQ交于点S．问：点S是否在同一直线上？若是，请求出这条直线的方程；若不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
