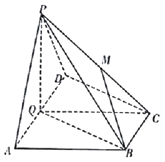
【题目】如图，在四棱锥
中，底面
为直角梯形， 
， 
，平面
底面
， 
为
的中点， 
是棱
上的点， 
， 
， 
.
（Ⅰ）求证：平面
平面
；
（Ⅱ）若异面直线
与
所成角的余弦值为
，求
的值.
【答案】（1）见解析（2）
或
.
【解析】试题分析：（1）推导出四边形BCDQ为平行四边形，从而CD∥BQ．又QB⊥AD．从而BQ⊥平面PAD，由此能证明平面PQB⊥平面PAD；（2）以Q为原点，QA为x轴，QB为y轴，QP为z轴，建立空间直角坐标系．利用向量法能求出t的值，即可得到比值。
解析：
（Ⅰ）证明：∵
， 
， 
为
的中点，
∴四边形
为平行四边形，∴
.
∵
，∴
，即
.
又∵平面
平面
，且平面
平面
.
∵
平面
.
∵
平面
，∴平面
平面
.
（Ⅱ）∵
， 
为
的中点，∴
.
∵平面
平面
，且平面
平面
.
∴
平面
.
如图，以
为原点建立空间直角坐标系，则
， 
， 
， 
， 
，设
，
∴
， 
， 
.
由
是
上的点，设
，化简得
.
设异面直线
与
所成角为
，
则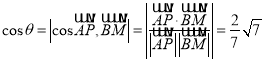
.
∴
，计算得
或
，故
或
.
注：若只算出一个答案，扣1分；算出两个
值即得满分.
科目：高中数学 来源： 题型：
【题目】已知函数
有极值，且函数
的极值点是
的极值点，其中
是自然对数的底数.（极值点是指函数取得极值时对应的自变量的值）
（1）求
关于
的函数关系式；
（2）当
时，若函数
的最小值为
，证明： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】了解某市今年初二年级男生的身体素质状况，从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格，成绩在6至8米（含6米不含8米）的为及格，成绩在8米至12米（含8米和12米，假定该市初二学生掷实心球均不超过12米）为优秀．把获得的所有数据，分成
五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在10米到12米之间．
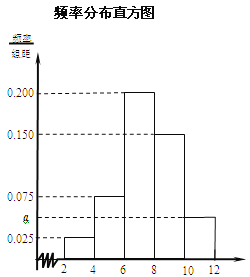
（Ⅰ）求实数
的值及参加“掷实心球”项目测试的人数；
（Ⅱ）根据此次测试成绩的结果，试估计从该市初二年级男生中任意选取一人，“掷实心球”成绩为优秀的概率；
（Ⅲ）若从此次测试成绩最好和最差的两组男生中随机抽取2 名学生再进行其它项目的测试，求所抽取的2名学生来自不同组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高二期中考试后，教务处计划对全年级数学成绩进行统计分析，从男、女生中各随机抽取100名学生，分别制成了男生和女生数学成绩的频率分布直方图，如图所示.
（1）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？
（2）在（1）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有1名男生的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市创业园区新引进一家生产环保产品的公司，已知该环保产品每售出1盒的利润为0.3万元，当月未售出的环保产品，每盒亏损0.12万元．根据统计资料，该环保产品的市场月需求量的频率分布直方图如图所示．
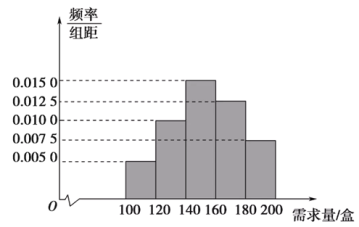
（1）若该环保产品的月进货量为160盒，以
（单位：盒，
）表示该产品一个月内的市场需求量，
（单位：万元）表示该公司生产该环保产品的月利润．
①将表示为的函数；
②根据频率分布直方图估计利润不少于39.6万元的概率．
（2）在频率分布直方图的月需求量分组中，以各组的区间中点值代表该组的月需求量，当月进货量为158箱时，写出月利润
（单位：万元）的所有可能值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
（cosx，2cosx），
（2cosx，sinx），f（x）
．
（1）把f（x）的图象向右平移
个单位得g（x）的图象，求g（x）的单调递增区间；
（2）当
与共线时，求f（x）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2018衡水金卷（三）】如图所示，在三棱锥
中，平面
平面
， 
， 
， 
， 
．
（I）证明： 
平面
；
（II）若二面角
的平面角的大小为
，求直线
与平面
所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
