Question

将一块圆心角为60°，半径为20cm的扇形铁电裁成一个矩形，求裁得矩形的最大面积．

Answer 1

分析：设∠PON=θ则可表示出PN和MN，进而根据矩形的面积公式表示出其面积表达式，利用三角函数的性质求得其最大值．

解答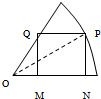：解：如图设∠PON=θ，则PN=20sinθ，MN=20cosθ-

20

3

sinθ，
S_MNPQ=20sinθ（20cosθ-

20

3

sinθ），
当θ=30°时，S_MNPQ取最大值

200 3

3

．
如图（2），设∠FOA=θ，则EF=40sin（30°-θ），在△OFG中，∠OGF=150°，故

FG

sinθ

=

R

sin150°

即FG=40sinθ
设矩形的面积为S．
那么S_矩形EFFG=1600sinθsin（30°-θ）
=800[cos（2θ-30°）-cos30°]=800[cos（2θ-30°）-

3

2

]
又∵0＜θ＜30°，故当cos（2θ-30°）=1即θ=15°时，S取最大值400（2-

3

），显然，

3

6

×400＞(2-

3

)×400，所以内接矩形的最大面积为

200 3

3

．

点评：本题主要考查了在实际问题中建立三角函数模型的问题．考查了考生运用所学知识解决实际问题的能力．