
【题目】已知命题P:函数f(x)=log2m(x+1)是增函数;命题Q:x∈R,x2+mx+1≥0.
(1)写出命题Q的否命题¬Q;并求出实数m的取值范围,使得命题¬Q为真命题;
(2)如果“P∨Q”为真命题,“P∧Q”为假命题,求实数m的取值范围
【答案】
(1)解:Q:x0∈R,x02+mx0+1<0.
若Q为真命题,则△=m2﹣4>0,解得:m<﹣2,或m>2.
故所求实数m的取值范围为:(﹣∞,﹣2)∪(2,+∞).
(2)解:若函数f(x)=log2m(x+1)是增函数,则 2m>1, ![]() .
.
又x∈R,x2+mx+1≥0为真命题时,由△=m2﹣4≤0,
求得m的取值范围为B={m|﹣2≤m≤2}.
由“P∨Q”为真命题,“P∧Q”为假命题,故命题P、Q中有且仅有一个真命题.
当P真Q假时,实数m的取值范围为:
![]() .
.
当P假Q真时,实数m的取值范围为:
![]() ;
;
综上可知实数m的取值范围:[﹣2, ![]() ]∪(2,+∞).
]∪(2,+∞).
【解析】(1)否命题Q,就是把命题Q的条件和结论都否定,联系对应二次函数图象,由△=m2﹣4>0,解得m的
取值范围.(2)命题P和命题Q中,一个为真命题,一个为假命题,分命题P是真命题且命题Q是假命题、命题P是
假命题且命题Q是真命题,两种情况,计算可得答案.
【考点精析】通过灵活运用交、并、补集的混合运算和对数函数的单调性与特殊点,掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法;过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数即可以解答此题.


科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面 ![]() 平面
平面 ![]() ,四边形
,四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.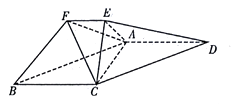
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求 ![]() 到平面
到平面 ![]() 的距离;
的距离;
(3)求三棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A′B′C′D′中:
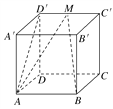
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为a,M为BD1的中点,N在A1C1上,且满足|A1N|=3|NC1|.
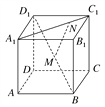
(1)求MN的长;
(2)试判断△MNC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在区间[t,t+2](t>0)上的最小值;
(2)对一切实数x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),lnx> ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ∥
∥![]() ;
;
③![]() 的体积是
的体积是![]() ;
;
④平面![]() ⊥平面
⊥平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中正确的有 .(填写你认为正确的序号)
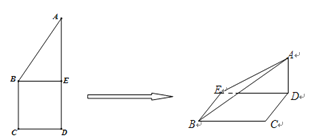
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x﹣1)的对称轴为x=1,f(x+1)= ![]() (f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
(f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
A.f(sinα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(sinα)=f(cosβ)
D.以上情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com