练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知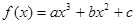的图象经过点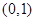，且在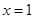处的切线方程是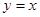
    （1）求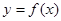的解析式；（2）求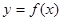的单调递增区间

    （1），（2）.

    解析试题分析：（1）求具体函数解析式基本方法为待定系数法.所求解析式有三个参数，需要三个独立条件.一是即，二是即，三是即，综合解得，（2）利用导数大于零求出函数对应增区间.函数定义域为一切实数，因此导数大于零对应的自变量取值范围为增区间，即由得，但单调区间必须是连续区间，因此单调增区间为两个，在每个区间上都是单调增，但在并集上不具有单调性.
    试题解析：（1）解： 的图象经过点，则，
    ,
    切点为，则的图象经过点
    得解得即      6分
    （2）得
    单调递增区间为                         10分
    考点：函数解析式，利用导数求单调区间

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    设函数
    （1）若关于x的不等式在有实数解，求实数m的取值范围；
    （2）设，若关于x的方程至少有一个解，求p的最小值．
    （3）证明不等式：    

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数.
    （1）当时，求曲线在点处的切线方程；
    （2）当时，讨论的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知.
    （1）求函数的最大值；
    （2）设，，且，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数（、为常数），在时取得极值.
    （1）求实数的值；
    （2）当时，求函数的最小值；
    （3）当时，试比较与的大小并证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝ax2－(4a＋2)x＋4lnx，其中a≥0．
    （1）若a＝0，求曲线y＝f(x)在点(1，f(1))处的切线方程；
    （2）讨论函数f(x)的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （Ⅰ）当在区间上的最大值和最小值；
    （Ⅱ）若在区间上，函数的图象恒在直线下方，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设，阴影部分为一公共设施建设不能开发，且要求用栏栅隔开(栏栅要求在一直线上)，公共设施边界为曲线f(x)＝1－ax2(a＞0)的一部分，栏栅与矩形区域的边界交于点M、N，交曲线于点P，设P(t，f(t))．
     
    (1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t)；
    (2)若在t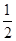＝处，S(t)取得最小值，求此时a的值及S(t)的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设f(x)＝，其中a为正实数．
    ①当a＝时，求f(x)的极值点；②若f(x)为R上的单调函数，求a的取值范围．

    查看答案和解析>>

    同步练习册答案