
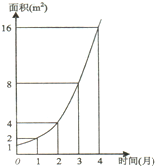
 近几年,每年11月初,黄浦江上漂浮在大片的水葫芦,严重影响了黄浦江的水利、水质、航运和市容景观.为了解决这个环境问题,科研人员进行科研攻关.如图是科研人员在实验室池塘中观察水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:
近几年,每年11月初,黄浦江上漂浮在大片的水葫芦,严重影响了黄浦江的水利、水质、航运和市容景观.为了解决这个环境问题,科研人员进行科研攻关.如图是科研人员在实验室池塘中观察水葫芦的面积与时间的函数关系图象.假设其函数关系为指数函数,并给出下列说法:

科目:高中数学 来源: 题型:
 某堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=H(10-
某堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=H(10-| 1 |
| 10 |
. |
| v |
. |
| v |
| A、t1 |
| B、t2 |
| C、t3 |
| D、t4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| x |
| x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
| 1 |
| e |
| f(x) |
| x |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com