
【题目】下列四个命题中,真命题有________.(写出所有真命题的序号)
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;
②命题“x0∈R,x+x0+1<0”的否定是“x∈R,x2+x+1≥0”;
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=ln x+x-![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
【答案】①②③④
【解析】①若c=0,则不论a,b的大小关系如何,都有ac2=bc2,而若ac2>bc2,则有a>b,故“ac2>bc2”是“a>b”成立的充分不必要条件,故①为真命题;②特称命题的否定是全称命题,故命题“x0∈R,x+x0+1<0”的否定是“x∈R,x2+x+1≥0”,故②为真命题;③命题“若p,则q”形式的命题的否命题是“若綈p,则綈q”,故命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”,故③为真命题;④由于f(1)f(2)=![]()
![]() =
=![]() ×
×![]() <0,则函数f(x)=ln x+x-
<0,则函数f(x)=ln x+x-![]() 在区间(1,2)上存在零点,又函数f(x)=ln x+x-
在区间(1,2)上存在零点,又函数f(x)=ln x+x-![]() 在区间(1,2)上为增函数,所以函数f(x)=ln x+x-
在区间(1,2)上为增函数,所以函数f(x)=ln x+x-![]() 在区间(1,2)上有且仅有一个零点,故④为真命题.
在区间(1,2)上有且仅有一个零点,故④为真命题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足: ![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若存在![]() ,使得
,使得![]() 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的![]() ,且
,且![]() 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三次函数![]() ,
,
(1)若函数![]() 过点
过点![]() 且在点
且在点![]() 处的切线方程是
处的切线方程是![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,
,
都有![]() ,求实数
,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
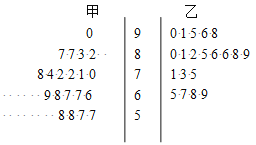
(1)学校规定:成绩不低于75分的为优秀.请画出下面的![]() 列联表.
列联表.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com